Flipkart limited interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Flipkart limited
3 rounds | 8 Coding
problems
Interview preparation journey
Preparation
Duration: 4 Months
Topics: Data Structures, Algorithms, System Design, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Medium
Video Call
Duration60 Minutes
Interview date18 Aug 2021
Coding problem3
The round was held on Google Meet and I was given 2 coding problems for which first I had to explain my approach and then I had to write code in Shared Google Docs and dry run on sample test cases and discuss Time and Space Complexity. After the coding problems , I was asked some basic theoretical concepts from Data Structures and Time Complexities.
There were 2 interviewers and both were very friendly and helpful and tried to bring us to our comfort level first.
1. Smallest Window
Moderate
10m average time
90% success
0/80
Asked in companies



You are given two strings S and X containing random characters. Your task is to find the smallest substring in S which contains all the characters present in X.
Example:
Let S = “abdd” and X = “bd”.
The windows in S which contain all the characters in X are: 'abdd', 'abd', 'bdd', 'bd'.
Out of these, the smallest substring in S which contains all the characters present in X is 'bd'.
All the other substring have a length larger than 'bd'.
Problem approach
Approach 1 (Brute Force) :
1) Generate all substrings of string1.
2) For each substring, check whether the substring contains all characters of string2.
3) Finally, print the smallest substring containing all characters of string2.
TC : O(N^3), where N=length of the given string s1 and s2
SC : O(1)
Approach 2 (Sliding Window) :
We can use a simple sliding window approach to solve this problem.
The solution is pretty intuitive. We keep expanding the window by moving the right pointer. When the window has all the desired characters, we contract (if possible) and save the smallest window till now.
The answer is the smallest desirable window.
Algorithm :
1) We start with two pointers, left and right initially pointing to the first element of the string S.
2) We use the right pointer to expand the window until we get a desirable window i.e. a window that contains all of the characters of T
3) Once we have a window with all the characters, we can move the left pointer ahead one by one. If the window is still a desirable one we keep on updating the minimum window size.
4) If the window is not desirable any more, we repeat step2 onwards.
TC : O(N+M) where N and M are the respective length of strings S and T.
SC : O(N+M)
2. Pythagorean Triplets
Moderate
35m average time
70% success
0/80
Asked in companies



You are given an array of n integers (a1, a2,....,an), you need to find if the array contains a pythagorean triplet or not.
An array is said to have a pythagorean triplet if there exists three integers x,y and z in the array such that x^2 + y^2 = z^2.
Note
1. The integers x,y and z might not be distinct , but they should be present at different locations in the array i.e if a[i] = x, a[j] = y and a[k] = z, then i,j and k should be pairwise distinct.
2. The integers a,b and c can be present in any order in the given array.
Problem approach
Approach 1 :
1) Sort the array
2) Initially map all the elements of the array to their index in a Hash Map or a Hash Set
3) Now , run 2 for loops and for every x^2 + y^2 ,check if there exists a z^2 s.t x^2+y^2=z^2 and the index of z^2 is different than both the indices of x and y.
TC : O(N^2), where N=size of the array
SC : O(N)
Approach 2 :
1 )We can use a hash map to mark all the values of the given array.
2) Using two loops, we can iterate for all the possible combinations of a and b, and then check if there exists the third value c.
3) If there exists any such value, then there is a Pythagorean triplet.
TC : O(max*max), where max is the maximum most element in the array
SC : O(N), where N = size of the array
3. DS Question
What is the complexity of retrieving min element from a max heap?
Problem approach
Answer :
The answer is O(n). In each step we need traverse both left and right sub-trees in order to search for the minimum element. In effect, this means that we need to traverse all elements to find the minimum.
02
Round
Medium
Video Call
Duration60 Minutes
Interview date18 Aug 2021
Coding problem3
This was also a Data Structures and Algorithms round where I was asked to solve 2 coding problems explaining my approach with proper Complexity Analysis . After the coding questions were over there was some time left so the interviewer asked me an interesting puzzle just to check my aptitude.
1. Find the median of all subarrays of a particular size
Moderate
30m average time
70% success
0/80
Asked in companies



You have been given an array/list ‘ARR’ of integers consisting of ‘N’ integers. You are also given a size ‘M’. You need to display the median of all the subarrays of size ‘M’ and it is starting from the very left of the array.
Median is the middle value in an ordered integer array/list. If the size of the array/list is even there is no middle element. So the median is the mean of two middle values in an even size array/list.
Your task is to return the median of all the subarrays whose size is ‘M’.
Example:
Let’s say you have an array/list [1,4,3,5] and ‘M’ is 3.Then the first subarray of size 3 is [1,4,3] whose median is 3.Then the second subarray of size 3 is [4,3,5] whose median is 4. Therefore the median of all the subarrays of size 3 is [3.0,4.0].
Problem approach
Approach 1 (Brute Force) :
Solve for each subarray individually.
Algorithm :
For a particular subarray of size ‘M’:-
1) Sort this subarray as we need to order the integers to find the subarray.
2) Median is calculated as follows:-
2.1) If ‘M’ is odd, the median is the m/2th element of the sorted subarray (0-based indexing is assumed).
3) Else the median is the mean of ‘(M/2-1)th’ and ‘M/2th’ element of the sorted subarray (0-based indexing is assumed).
4) Push the median into the ‘ANS’ vector/list.
TC : O(N * M * log(M)), where ‘N’ denotes the size of array/list and ‘M’ denotes size of the subarray.
SC : O(M), where ‘M’ denotes the size of the subarray.
Approach 2 (Using Multiset) :
We use multiset(self-balance binary tree) because it keeps elements in sorted order and can have multiple occurrences of a number. Declare a multiset 'WINDOWS'.
Algorithm :
1) Insert first 'M' elements in multiset 'WINDOWS'.
2) Calculate median as the mean of value at this iterator and 'M/2-1 + M%2'th position. In case 'M' is odd both iterators point to the same element.
3) In case 'M' is even first iterator points to 'M/2'th element and the second iterator points to ‘M/2-1’th element.
4) We iterate from 'M' to 'N'-1 for the rest of the subarrays.
5) In each iteration:-
5.1) We remove ‘ARR[i-m]’ from multiset:-
If it is less than mid we decrease iterator 'MID' by ‘1’.
5.2) We insert ‘ARR[i]’ in multiset:-
If it is less than equal to mid we increase iterator 'MID' by ‘1’.
5.3) Calculate 'MEDIAN' in a similar way as described for the first subarray.
6) Finally, we return the array/list ‘ANS’.
TC : O(N * log(M)), where ‘N’ denotes the size of the array/list.
SC : O(M), where ‘M’ denotes the size of the subarray.
2. Validate BST
Moderate
25m average time
70% success
0/80
Asked in companies



Given a binary tree with N number of nodes, check if that input tree is Partial BST (Binary Search Tree) or not. If yes, return true, return false otherwise.
A binary search tree (BST) is said to be a Partial BST if it follows the following properties.
• The left subtree of a node contains only nodes with data less than and equal to the node’s data.
• The right subtree of a node contains only nodes with data greater than and equal to the node’s data.
• Both the left and right subtrees must also be partial binary search trees.
Example:
Input:
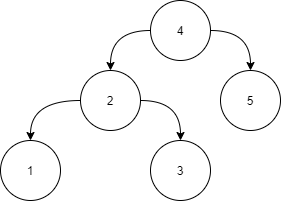
Answer:
Level 1:
All the nodes in the left subtree of 4 (2, 1, 3) are smaller
than 4, all the nodes in the right subtree of the 4 (5) are
larger than 4.
Level 2 :
For node 2:
All the nodes in the left subtree of 2 (1) are smaller than
2, all the nodes in the right subtree of the 2 (3) are larger than 2.
For node 5:
The left and right subtree for node 5 is empty.
Level 3:
For node 1:
The left and right subtree for node 1 are empty.
For node 3:
The left and right subtree for node 3 are empty.
Because all the nodes follow the property of a Partial binary
search tree, the above tree is a Partial binary search tree.
Problem approach
Approach 1 (Recursive Inorder Traversal) :
We know that the inorder traversal of a BST always gives us a sorted array , so if we maintain two variable Tree Nodes "previous" and "current" , we should always have previous->val < current->value for a valid BST.
Steps :
1) Create a boolean recursive function with two parameters (root and prev) which will return true if our binary tree is a BST or else it will return false.
2) If root is not null , call the recursive function with parameters (root->left,prev) and check if it return true or not.
3) For the prev node , check if at any point prev->val >= root->val if this condition is met , simply return false.
4) Update prev with root.
5) Call the recursive function again with parameters (root->right , prev)
TC : O(N) where N=number of nodes in the binary tree
SC : O(N)
//Pseudo Code :
bool isValidBST2(TreeNode* root , TreeNode*&prev)
{
//Using inorder traversal
if(root)
{
if(!isValidBST2(root->left,prev))
return false;
if(prev and prev->val >= root->val)
return false;
prev=root;
return isValidBST2(root->right,prev);
}
return true;
}
bool isValidBST(TreeNode*root)
{
TreeNode*prev=NULL;
return isValidBST2(root,prev);
}
Approach 2 (Iterative Inorder Traversal) :
We can also perfom an iterative inorder traversal of the Binary Tree using a stack and check the same condition that we checked above i.e., at any point if prev->value >= current->value if this is met then simply return false.
Steps :
1) Take a stack of TreeNodes and a TreeNode prev with its initial value as NULL.
2) Run a loop till stack is not empty or root != NULL.
3) While pushing a root to the stack, push all its left descendants into the stack untill root != NULL.
4) Take current = stack.top() and pop it from the stack
5) Check if prev is NOT NULL and if prev->val >= curr->val , if this cond. is met simply return false.
6) Update prev with current.
7) Update root with root->right.
TC : O(N) where N=number of nodes in the binary tree
SC : O(N)
//Pseudo Code :
bool isValidBST(TreeNode* root)
{
stackst;
TreeNode*prev=NULL;
while(!st.empty() || root!=NULL)
{
while(root!=NULL)
{
st.push(root);
root=root->left;
}
root=st.top();
st.pop();
if(prev and prev->val>=root->val)
return false;
prev=root;
root=root->right;
}
return true;
}
3. Puzzle
Mislabeled Jars :
There are 3 jars, namely, A, B, C. All of them are mislabeled. Following are the labels of each of the jars:
A: Candies
B: Sweets
C: Candies and Sweets (mixed in a random proportion)
You can put your hand in a jar and pick only one eatable at a time. Tell the minimum number of eatable(s) that has/have to be picked in order to label the jars correctly.
Problem approach
Answer : 1 pick of an eatable is required to correctly label the Jars.
Approach :
1) Pick only one eatable from jar C. Suppose the eatable is a candy, then the jar C contains candies only(because all the jars were mislabeled).
2) Now, since the jar C has candies only, Jar B can contain sweets or mixture. But, jar B can contain only the mixture because its label reads “sweets” which is wrong.
3) Therefore, Jar A contains sweets. Thus the correct labels are:
A : Sweets.
B : Candies and Sweets.
C : Candies.
03
Round
Medium
Video Call
Duration50 Minutes
Interview date18 Aug 2021
Coding problem2
In this round I was first asked to implement a Phone Book , which required the knowledge of Trie and then I was asked a question related to Memory Management and External Sorting . I was able to answer both of them with proper explanation and codes.
1. Implement a phone directory
Hard
50m average time
50% success
0/120
Asked in companies



You are given a list/array of strings which denotes the contacts that exist in your phone directory. The search query on a string ‘str’ which is a query string displays all the contacts which are present in the given directory with the prefix as ‘str’. One special property of the search function is that when a user searches for a contact from the contact list then suggestions (contacts with prefix as the string entered so for) are shown after the user enters each character.
Note :
If no suggestions are found, return an empty 2D array.
For Example :
In the above example everytime we enter a character, a few suggestions display the strings which contain the entered string as prefixes.
Problem approach
Approach :
Phone Directory can be efficiently implemented using Trie Data Structure.
1) We insert all the contacts into Trie.
2) Generally search query on a Trie is to determine whether the string is present or not in the trie, but in this case we are asked to find all the strings with each prefix of ‘str’. This is equivalent to doing a DFS traversal on a graph.
3) From a Trie node, visit adjacent Trie nodes and do this recursively until there are no more adjacent. This recursive function will take 2 arguments one as Trie Node which points to the current Trie Node being visited and other as the string which stores the string found so far with prefix as ‘str’.
4) Each Trie Node stores a boolean variable ‘isLast’ which is true if the node represents end of a contact(word).
5) User will enter the string character by character and we need to display suggestions with the prefix formed after every entered character.
6) Find the prefix starting with the string formed is to check if the prefix exists in the Trie, if yes then call the displayContacts() function. In this approach after every entered character we check if the string exists in the Trie.
7) Instead of checking again and again, we can maintain a pointer prevNode‘ that points to the TrieNode which corresponds to the last entered character by the user, now we need to check the child node for the ‘prevNode’ when user enters another character to check if it exists in the Trie.
8) If the new prefix is not in the Trie, then all the string which are formed by entering characters after ‘prefix’ can’t be found in Trie too.
9) So we break the loop that is being used to generate prefixes one by one and print “No Result Found” for all remaining characters.
2. Counting Sort
Easy
0/40
Asked in companies



Ninja is studying sorting algorithms. He has studied all comparison-based sorting algorithms and now decided to learn sorting algorithms that do not require comparisons.
He was learning counting sort, but he is facing some problems. Can you help Ninja implement the counting sort?
For example:
You are given ‘ARR’ = {-2, 1, 2, -1, 0}. The sorted array will be {-2, -1, 0, 1, 2}.
Problem approach
- The maximum element of the initial array is stored in variable ‘K’
- ‘Count’ array is created with all elements initially being 0, and then the count is incremented every time the number at the index occurs in the array.
- ‘Count’ array is updated for positions by taking the sum of previous elements and storing it as the position for the sorted array.
- Elements are put into the sorted array using a for loop and the function is finally called for sorting a given array.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
3 rounds | 10 problems
Interviewed by Flipkart limited
2615 views
0 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Flipkart limited
1173 views
0 comments
0 upvotes
SDE - 1
3 rounds | 3 problems
Interviewed by Flipkart limited
1686 views
0 comments
0 upvotes
SDE - 1
3 rounds | 4 problems
Interviewed by Flipkart limited
2170 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114869 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58030 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35057 views
7 comments
0 upvotes





