Flipkart limited interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Flipkart limited
3 rounds | 10 Coding
problems
Interview preparation journey
Preparation
Duration: 4 Months
Topics: Data Structures, Algorithms, System Design, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Medium
Video Call
Duration50 Minutes
Interview date12 Jul 2021
Coding problem3
The round was held on Google Meet and I was given 2 coding problems for which first I had to explain my approach and then I had to write code in Shared Google Docs and dry run on sample test cases and discuss Time and Space Complexity. After the coding problems , I was asked some basic theoretical concepts from Data Structures and Time Complexities.
There were 2 interviewers and both were very friendly and helpful and tried to bring us to our comfort level first.
1. Add two number as linked lists
Moderate
10m average time
80% success
0/80
Asked in companies



You have been given two singly Linked Lists, where each of them represents a positive number without any leading zeros.
Your task is to add these two numbers and print the summation in the form of a linked list.
Example:
If the first linked list is 1 -> 2 -> 3 -> 4 -> 5 -> NULL and the second linked list is 4 -> 5 -> NULL.
The two numbers represented by these two lists are 12345 and 45, respectively. So, adding these two numbers gives 12390.
So, the linked list representation of this number is 1 -> 2 -> 3 -> 9 -> 0 -> NULL.
Problem approach
Approach :
1) Calculate sizes of given two linked lists.
2) If sizes are same, then calculate sum using recursion. Hold all nodes in recursion call stack till the rightmost node, calculate the sum of rightmost nodes and forward carry to the left side.
3) If size is not same, then follow below steps:
a) Calculate difference of sizes of two linked lists. Let the difference be diff
b) Move diff nodes ahead in the bigger linked list. Now use step 2 to calculate the sum of the smaller
list and right sub-list (of the same size) of a larger list. Also, store the carry of this sum.
c) Calculate the sum of the carry (calculated in the previous step) with the remaining left sub-list of a
larger list. Nodes of this sum are added at the beginning of the sum list obtained the previous step.
TC : O(m+n) where m=Length of Linked List 1 and n=Length of Linked List 2
SC : O(m+n)
2. Maximum sum path from the leaf to root
Easy
10m average time
90% success
0/40
Asked in companies



You are given a binary tree of 'N' nodes.
Your task is to find the path from the leaf node to the root node which has the maximum path sum among all the root to leaf paths.
For Example:
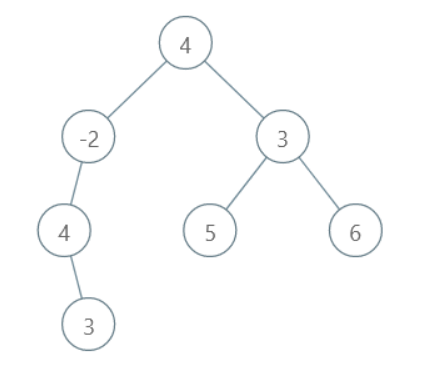
All the possible root to leaf paths are:
3, 4, -2, 4 with sum 9
5, 3, 4 with sum 12
6, 3, 4 with sum 13
Here, the maximum sum is 13. Thus, the output path will be 6, 3, 4.
Note:
There will be only 1 path with max sum.
Problem approach
Approach :
The approach is as follows:
1) Get the max sum path for the left subtree.
2) Get the max sum path for the right subtree.
3) Select the one with the max sum from both and insert current node's data into it.
4) Return the updated path.
Algorithm:
list ‘MAXPATHSUM’('ROOT'):
1) If the root is NULL: return empty list.
2) Initialize ‘LEFTPATH’ = ‘MAXPATHSUM’('ROOT'->left).
3) Initialize ‘LEFTPATH’ = ‘MAXPATHSUM’('ROOT'->right).
4) Append 'ROOT' -> data to both the lists.
5) Find the sum of both lists.
6) Return the list with the greater sum.
TC : O(N+H^2), where ‘N’ is the number of nodes in the Binary tree and ‘H’ is the height of the binary tree.
SC : O(N)
3. DS Question
What is the complexity of retrieving min element from a max heap
Problem approach
Answer :
The answer is O(n). In each step we need traverse both left and right sub-trees in order to search for the minimum element. In effect, this means that we need to traverse all elements to find the minimum.
02
Round
Medium
Video Call
Duration50 Minutes
Interview date12 Jul 2021
Coding problem3
This was also a Data Structures and Algorithm round where I was asked to solve 2 medium to hard level problems along with their pseudo code within 50 minutes . Later I was also tested on some basic questions related to Sorting Algorithms.
1. Kth ancestor of a node in binary tree
Hard
50m average time
35% success
0/120
Asked in companies



You are given an arbitrary binary tree consisting of N nodes numbered from 1 to N, an integer 'K', and a node 'TARGET_NODE_VAL' from the tree. You need to find the Kth ancestor of the node 'TARGET_NODE_VAL'. If there is no such ancestor, then print -1.
The Kth ancestor of a node in a binary tree is the Kth node in the path going up from the given node to the root of the tree. Refer to sample test cases for further explanation.
Note:
1. The given node 'TARGET_NODE_VAL' is always present in the tree.
2. The value of each node in the tree is unique.
3. Notice that the Kth ancestor node if present will always be unique.
Problem approach
This was one of the most challenging problems I faced in all these rounds combined . It was based on Dynamic Programming and Trees . There is a technique called Binary Lifting that I cam across while solving problems on LeetCode and CodeStudio . This question was actually a direct implementation of this technique .
Steps :
Given we can have at most 2^20 th ancestor of a node
1) Initialise a 2D ancestor matrix where ancestor[node][i] = stores the 2^i th ancestor of the node in the binary tree
2) Recursively fill the ancestor table in a Top-Down manner.
3)Once the ancestor table is filled , run a loop from i=19 to i=0 and check if 2^i <= k .
4) If 2^i<=k , then node=ancetor[node][i] and do k-=2^i
5) If at any point node==-1 , simply return -1
6) Finally return the answe node
TC : O(log(N))
SC : O(N)
//Psuedo Code :
int n;
vectoradj[50001];
int ancestor[50001][20]; //ancestor[node][i] := stores the 2^i ancestor of node
void calcAncestor(int node , int par)
{
ancestor[node][0]=par;
for(int i=1; i<20; i++)
{
if(ancestor[node][i-1]!=-1)
ancestor[node][i]=ancestor[ancestor[node][i-1]][i-1];
else
ancestor[node][i]=-1;
}
for(auto child : adj[node])
{
if(child!=par)
calcAncestor(child,node);
}
}
TreeAncestor(int N, vector& par)
{
n=N;
for(int i=0; i= 0; i--)
{
int num = (1<= num)
{
node = ancestor[node][i];
k -= num;
if(node == -1) return -1;
}
}
return node;
}
2. Find All Triplets With Zero Sum
Moderate
30m average time
50% success
0/80
Asked in companies



You are given an array Arr consisting of n integers, you need to find all the distinct triplets present in the array which adds up to zero.
An array is said to have a triplet {arr[i], arr[j], arr[k]} with 0 sum if there exists three indices i, j and k such that i!=j, j!=k and i!=k and arr[i] + arr[j] + arr[k] = 0.
Note :
1. You can return the list of values in any order. For example, if a valid triplet is {1, 2, -3}, then (2, -3, 1), (-3, 2, 1) etc is also valid triplet. Also, the ordering of different triplets can be random i.e if there are more than one valid triplets, you can return them in any order.
2. The elements in the array need not be distinct.
3. If no such triplet is present in the array, then return an empty list, and the output printed for such a test case will be "-1".
Problem approach
Approach 1 (Naive) :
The naive approach runs three loops and check one by one that sum of three elements is zero or not. If the sum of three elements is zero then print elements otherwise print not found.
Algorithm:
1) Run three nested loops with loop counter i, j, k.
2) The first loops will run from 0 to n-3 and second loop from i+1 to n-2 and the third loop from j+1 to n-1. The loop counter represents the three elements of the triplet.
3) Check if the sum of elements at i’th, j’th, k’th is equal to zero or not. If yes print the sum else continue.
TC : O(N^3) where N=size of the array
SC : O(1)
Approach 2 (Using Hash Map - Time Efficient) :
This involves traversing through the array. For every element arr[i], find a pair with sum “-arr[i]”. This problem reduces to pair sum and can be solved in O(n) time using hashing.
Algorithm:
1) Create a hashmap to store a key-value pair.
2) Run a nested loop with two loops, the outer loop from 0 to n-2 and the inner loop from i+1 to n-1
3) Check if the sum of ith and jth element multiplied with -1 is present in the hashmap or not
4) If the element is present in the hashmap, print the triplet else insert the j’th element in the hashmap.
TC : O(N^2)
SC : O(N)
Approach 3 (Using Sorting - Time as well as Space Efficient) :
For every element check that there is a pair whose sum is equal to the negative value of that element.
Algorithm:
1) Sort the array in ascending order.
2) Traverse the array from start to end.
3) For every index i, create two variables l = i + 1 and r = n – 1
4) Run a loop until l is less than r if the sum of array[i], array[l] and array[r] is equal to zero then print the triplet and break the loop
5) If the sum is less than zero then increment the value of l, by increasing the value of l the sum will increase as the array is sorted, so array[l+1] > array [l]
6) If the sum is greater than zero then decrement the value of r, by increasing the value of l the sum will decrease as the array is sorted, so array[r-1] < array [r].
TC : O(N^2)
SC : O(1)
3. DS Question
Which is the fastest method to sort an almost sorted array: Insertion Sort , Quick Sort , Bubble Sort , Merge Sort , Shell Sort ?
Problem approach
Answer :
1) For sorting nearly sorted data , Insertion Sort is the best as it adapts to O(n) time when the data is nearly sorted.
2) Bubble sort is fast, but insertion sort has lower overhead.
3) Shell sort is fast because it is based on insertion sort.
4) Merge sort, heap sort, and quick sort do not adapt to nearly sorted data.
Insertion sort provides a O(n^2) worst case algorithm that adapts to O(n) time when the data is nearly sorted. One would like an O(n·lg(n)) algorithm that adapts to this situation; smoothsort is such an algorithm, but is complex. Shell sort is the only sub-quadratic algorithm that is also adaptive in this case.
03
Round
Medium
Video Call
Duration50 minutes
Interview date12 Jul 2021
Coding problem4
This round was also held on Google Meet where I was supposed to code 2 problems in a Google Doc. After the coding questions , I was asked some core concepts related to OS .
Both the interviewers were quite friendly and helpful. Overall it was a good experience.
1. Reverse Linked List
Easy
15m average time
85% success
0/40
Asked in companies



You are given a Singly Linked List of integers. You need to reverse the Linked List by changing the links between nodes.
Note :
You do not need to print anything, just return the head of the reversed linked list.
Problem approach
Iterative(Without using stack):
1) Initialize three pointers prev as NULL, curr as head and next as NULL.
2) Iterate through the linked list. In loop, do following.
// Before changing next of current,
// store next node
next = curr->next
// Now change next of current
// This is where actual reversing happens
curr->next = prev
// Move prev and curr one step forward
prev = curr
curr = next
3)Finally the prev pointer contains our head , i,e. ,head=prev .
TC : O(n) where n=length of the Linked List
SC: O(1)
Recursive:
1) Divide the list in two parts - first node and rest of the linked list.
2) Call reverse for the rest of the linked list.
3) Link rest to first.
4) Fix head pointer
TC:O(n)
SC:O(n)
Iterative(Using Stack):
1) Store the nodes(values and address) in the stack until all the values are entered.
2) Once all entries are done, Update the Head pointer to the last location(i.e the last value).
3) Start popping the nodes(value and address) and store them in the same order until the stack is empty.
4) Update the next pointer of last Node in the stack by NULL.
TC: O(n)
SC:O(n)
2. Find K-th smallest Element in BST
Easy
15m average time
85% success
0/40
Asked in companies



Given a binary search tree and an integer ‘K’. Your task is to find the ‘K-th’ smallest element in the given BST( binary search tree).
BST ( binary search tree) -
If all the smallest nodes on the left side and all the greater nodes on the right side of the node current node.
Example -

Order of elements in increasing order in the given BST is - { 2, 3, 4, 5, 6, 7, 8, 10 }
Suppose given ‘K = 3’ then 3rd smallest element is ‘4’.
Suppose given ‘K = 8’ then 8th smallest element is ‘10’.
Note:
1. You are not required to print the output explicitly, it has already been taken care of. Just implement the function and return the ‘K-th’ smallest element of BST.
2. You don’t need to return ‘K-th’ smallest node, return just value of that node.
3. If ‘K-th’ smallest element is not present in BST then return -1.
Problem approach
Approach 1 : Recursive Inorder Traversal
Steps :
1) The Inorder Traversal of a BST traverses the nodes in increasing order.
2) The idea is to build an inorder traversal of BST which is an array sorted in the ascending order.
3) Now the answer is the k - 1th element of this array.
TC : O(N) where N=number of nodes in the BST
SC : O(N)
Approach 2 : Iterative Inorder Traversal
Steps :
1) The above recursion could be converted into iteration, with the help of stack.
2) This way one could speed up the solution because there is no need to build the entire inorder traversal, and one could stop after the kth element.
TC : O(H) where H=height of the tree
SC : O(H)
3. OS Question
What do you mean by FCFS?
Problem approach
Answer :
1) FCFS (First Come First Serve) is a type of OS scheduling algorithm that executes processes in the same order in which processes arrive.
2) In simple words, the process that arrives first will be executed first. It is non-preemptive in nature.
3) FCFS scheduling may cause the problem of starvation if the burst time of the first process is the longest among all the jobs.
4) Burst time here means the time that is required in milliseconds by the process for its execution.
5) It is also considered the easiest and simplest OS scheduling algorithm as compared to others.
6) Implementation of FCFS is generally managed with help of the FIFO (First In First Out) queue.
4. OS Question
What is thrashing in OS?
Problem approach
Answer :
1) It is generally a situation where the CPU performs less productive work and more swapping or paging work.
2) It spends more time swapping or paging activities rather than its execution.
3) By evaluating the level of CPU utilization, a system can detect thrashing.
4) It occurs when the process does not have enough pages due to which the page-fault rate is increased. 5) It inhibits much application-level processing that causes computer performance to degrade or collapse.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
3 rounds | 7 problems
Interviewed by Flipkart limited
1172 views
0 comments
0 upvotes
SDE - 1
3 rounds | 3 problems
Interviewed by Flipkart limited
1884 views
0 comments
0 upvotes
SDE - 1
3 rounds | 3 problems
Interviewed by Flipkart limited
1686 views
0 comments
0 upvotes
SDE - 1
3 rounds | 4 problems
Interviewed by Flipkart limited
2170 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114868 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58030 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35056 views
7 comments
0 upvotes





