Software Engineer

You are given a Binary Tree.

Return the length of the diameter of the tree.

Note :

The diameter of a binary tree is the length of the longest path between any two end nodes in a tree.

The number of edges between two nodes represents the length of the path between them.

Example :

Input: Consider the given binary tree:

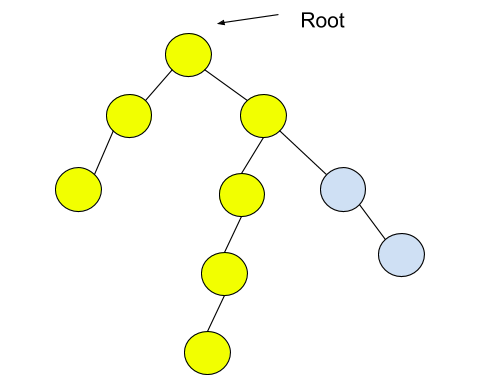
Output: 6

Explanation:
Nodes in the diameter are highlighted. The length of the diameter, i.e., the path length, is 6.

Make a fair coin from a biased coin.

You are given a function foo() that represents a biased coin. When foo() is called, it returns 0 with 60% probability, and 1 with 40% probability. Write a new function that returns 0 and 1 with a 50% probability each. Your function should use only foo(), no other library method.

You have been given two strings 'STR1' and 'STR2'. You have to check whether the two strings are anagram to each other or not.

Note:

Two strings are said to be anagram if they contain the same characters, irrespective of the order of the characters.

Example :

If 'STR1' = “listen” and 'STR2' = “silent” then the output will be 1.

Both the strings contain the same set of characters.

You are given an array 'arr' of length 'n'. Find the index(0-based) of a peak element in the array. If there are multiple peak numbers, return the index of any peak number.

Peak element is defined as that element that is greater than both of its neighbors. If 'arr[i]' is the peak element, 'arr[i - 1]' < 'arr[i]' and 'arr[i + 1]' < 'arr[i]'.

Assume 'arr[-1]' and 'arr[n]' as negative infinity.

Note:

1.  There are no 2 adjacent elements having same value (as mentioned in the constraints).
2.  Do not print anything, just return the index of the peak element (0 - indexed).
3. 'True'/'False' will be printed depending on whether your answer is correct or not.

Example:

Input: 'arr' = [1, 8, 1, 5, 3]

Output: 3

Explanation: There are two possible answers. Both 8 and 5 are peak elements, so the correct answers are their positions, 1 and 3.

Given two sorted arrays 'a' and 'b' of size 'n' and 'm' respectively.

Find the median of the two sorted arrays.

Median is defined as the middle value of a sorted list of numbers. In case the length of list is even, median is the average of the two middle elements.

The expected time complexity is O(min(logn, logm)), where 'n' and 'm' are the sizes of arrays 'a' and 'b', respectively, and the expected space complexity is O(1).

Example:

Input: 'a' = [2, 4, 6] and 'b' = [1, 3, 5]

Output: 3.5

Explanation: The array after merging 'a' and 'b' will be { 1, 2, 3, 4, 5, 6 }. Here two medians are 3 and 4. So the median will be the average of 3 and 4, which is 3.5.

You are given ‘N’ 2-D matrices and an array/list “ARR” of length ‘N + 1’ where the first ‘N’ integers denote the number of rows in the Matrices and the last element denotes the number of columns of the last matrix. For each matrix, the number of columns is equal to the number of rows of the next matrix. You are supposed to find the minimum number of multiplication operations that need to be performed to multiply all the given matrices.

Note :

You don’t have to multiply the matrices, you only have to find the minimum number of multiplication operations.

For Example :

ARR = {2, 4, 3, 2}

Here, we have three matrices with dimensions {2X4, 4X3, 3X2} which can be multiplied in the following ways:
a. If the order of multiplication is (2X4, 4X3)(3X2), then the total number of multiplication operations that need to be performed are: (2*4*3) + (2*3*2) = 36

b. If the order of multiplication is (2X4)(4X3, 3X2), then the total number of multiplication operations that need to be performed are  (2*4*2) + (4*3*2) = 40