SDE - 1

You are given a string ‘S’ of length ‘N’.

You must return the longest palindromic substring in ‘S’.

Note: Return any of them in case of multiple substrings with the same length.

Example:

Input: ‘S’ =’badam’

Output: ‘ada’

‘ada’ is the longest palindromic substring, and it can be proved that it is the longest possible palindromic substring.

You are given a positive integer 'N’. Your task is to find and return the minimum number of steps that 'N' has to take to get reduced to 1.

You can perform any one of the following 3 steps:

1) Subtract 1 from it. (n = n - ­1) ,
2) If n is divisible by 2, divide by 2.( if n % 2 == 0, then n = n / 2 ) ,
3) If n is divisible by 3, divide by 3. (if n % 3 == 0, then n = n / 3 ).

For example:

Given:
‘N’ = 4, it will take 2 steps to reduce it to 1, i.e., first divide it by 2 giving 2 and then subtract 1, giving 1.

Consider a directed graph of ‘N’ nodes where each node is labeled from ‘0’ to ‘N - 1’. Each edge of the graph is either ‘red’ or ‘blue’ colored. The graph may contain self-edges or parallel edges. You are given two arrays, ‘redEdges’ and ‘blueEdges’, whose each element is of the form [i, j], denoting an edge from node ‘i’ to node ‘j’ of the respective color.

Your task is to compute an array ‘answer’ of size ‘N’, where ‘answer[i]’ stores the length of the shortest path from node ‘0’ to node ‘i’ such that the edges along the path have alternate colors. If there is no such path from node ‘0’ to ‘i’, then ‘answer[i] = -1’.

Example:

N = 4, redEdges = [[0, 1], [2, 3]], blueEdges = [[1, 2], [1, 3]]

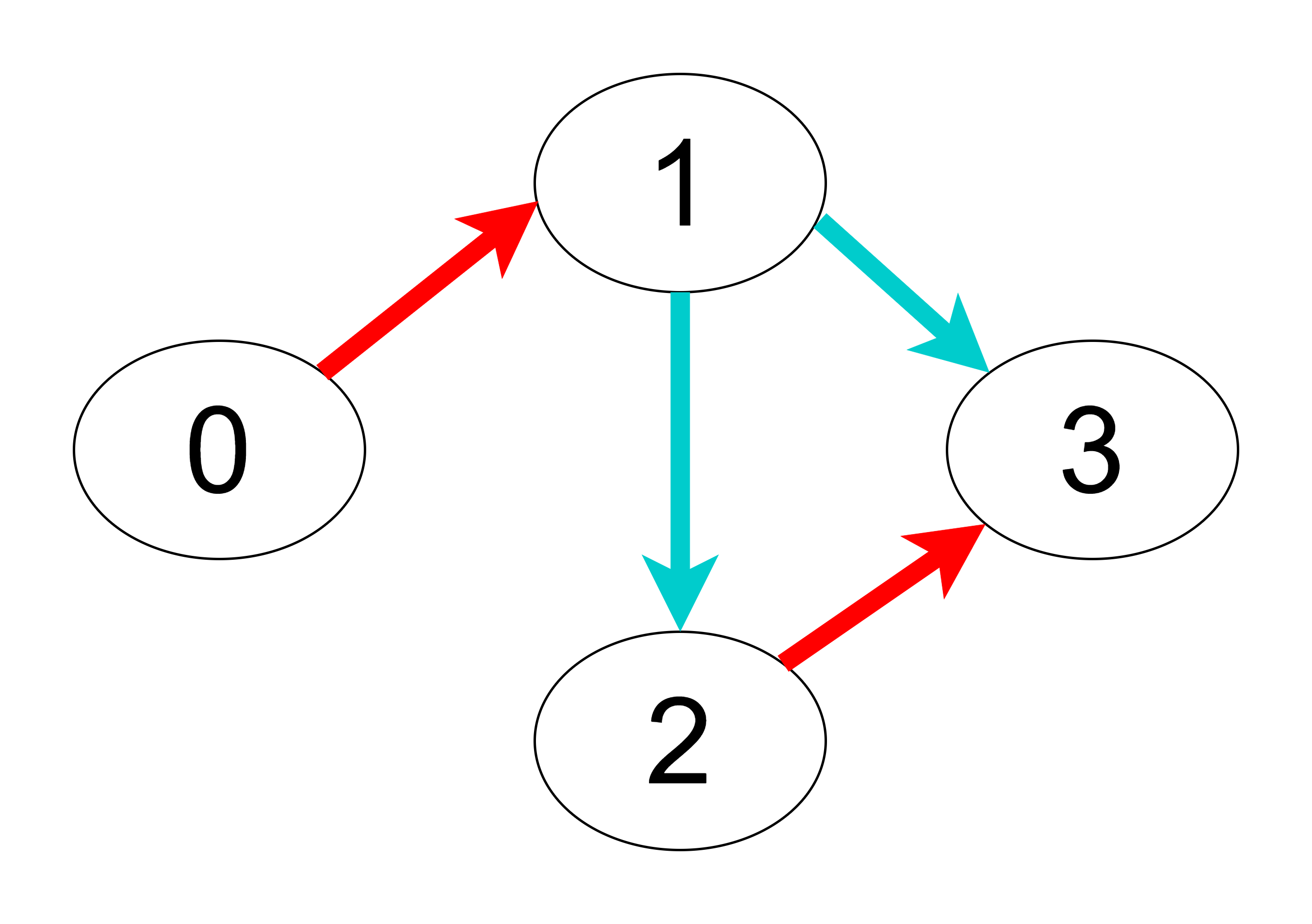
The shortest paths for each node from node ‘0’ are:
1: 0->1         Length: 1
2: 0->1->2      Length: 2
3: 0->1->3      Length: 2
So, the ‘answer’ array will be: [0, 1, 2, 2].

Note:

1. The given graph could be a disconnected graph.

2. Any two nodes ‘i’ and ‘j’ can have at most one red edge from ‘i’ to ‘j’ and at most one blue edge from ‘i’ to ‘j’.

You have given a sorted array 'A' of 'N' integers.

Now, you are given 'Q' queries, and each query consists of a single integer 'X'. Your task is to check whether 'X' is present in array 'A' or not for each query. If 'X' exists in array 'A', you need to print 1 else print 0.

Note :

The given array is sorted in non-decreasing order.