Trainee Software Engineer

Ninja has been given two sorted integer arrays/lists ‘ARR1’ and ‘ARR2’ of size ‘M’ and ‘N’. Ninja has to merge these sorted arrays/lists into ‘ARR1’ as one sorted array. You may have to assume that ‘ARR1’ has a size equal to ‘M’ + ‘N’ such that ‘ARR1’ has enough space to add all the elements of ‘ARR2’ in ‘ARR1’.

For example:

‘ARR1’ = [3 6 9 0 0]
‘ARR2’ = [4 10]
After merging the ‘ARR1’ and ‘ARR2’ in ‘ARR1’. 
‘ARR1’ = [3 4 6 9 10]

You are given two strings 'str1' and 'str1'.

You have to tell whether these strings form an anagram pair or not.

The strings form an anagram pair if the letters of one string can be rearranged to form another string.

Pre-requisites:

Anagrams are defined as words or names that can be formed by rearranging the letters of another word. Such as "spar" can be formed by rearranging letters of "rasp". Hence, "spar" and "rasp" are anagrams. 

Other examples include:

'triangle' and 'integral'
'listen' and 'silent'

Note:

Since it is a binary problem, there is no partial marking. Marks will only be awarded if you get all the test cases correct. 

You are given a 'Binary Tree'.

Return the bottom view of the binary tree.

Note :

1. A node will be in the bottom-view if it is the bottom-most node at its horizontal distance from the root. 

2. The horizontal distance of the root from itself is 0. The horizontal distance of the right child of the root node is 1 and the horizontal distance of the left child of the root node is -1. 

3. The horizontal distance of node 'n' from root = horizontal distance of its parent from root + 1, if node 'n' is the right child of its parent.

4. The horizontal distance of node 'n' from root = horizontal distance of its parent from the root - 1, if node 'n' is the left child of its parent.

5. If more than one node is at the same horizontal distance and is the bottom-most node for that horizontal distance, including the one which is more towards the right.

Example:

Input: Consider the given Binary Tree:

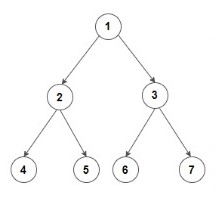
Output: 4 2 6 3 7

Explanation:
Below is the bottom view of the binary tree.

1 is the root node, so its horizontal distance = 0.
Since 2 lies to the left of 0, its horizontal distance = 0-1= -1
3 lies to the right of 0, its horizontal distance = 0+1 = 1
Similarly, horizontal distance of 4 = Horizontal distance of 2 - 1= -1-1=-2
Horizontal distance of 5 = Horizontal distance of 2 + 1=  -1+1 = 0
Horizontal distance of 6 = 1-1 =0
Horizontal distance of 7 = 1+1 = 2

The bottom-most node at a horizontal distance of -2 is 4.
The bottom-most node at a horizontal distance of -1 is 2.
The bottom-most node at a horizontal distance of 0 is 5 and 6. However, 6 is more towards the right, so 6 is included.
The bottom-most node at a horizontal distance of 1 is 3.
The bottom-most node at a horizontal distance of 2 is 7.

Hence, the bottom view would be 4 2 6 3 7

Given an array/list of length ‘n’, where the array/list represents the boards and each element of the given array/list represents the length of each board. Some ‘k’ numbers of painters are available to paint these boards. Consider that each unit of a board takes 1 unit of time to paint.

You are supposed to return the area of the minimum time to get this job done of painting all the ‘n’ boards under a constraint that any painter will only paint the continuous sections of boards.

Example :

Input: arr = [2, 1, 5, 6, 2, 3], k = 2

Output: 11

Explanation:
First painter can paint boards 1 to 3 in 8 units of time and the second painter can paint boards 4-6 in 11 units of time. Thus both painters will paint all the boards in max(8,11) = 11 units of time. It can be shown that all the boards can't be painted in less than 11 units of time.

You are given three strings 'A', 'B' and 'C'. Check whether 'C' is formed by an interleaving of 'A' and 'B'.

'C' is said to be interleaving 'A' and 'B', if the length of 'C' is equal to the sum of the length of 'A' and length of 'B', all the characters of 'A' and 'B' are present in 'C' and the order of all these characters remains the same in all three strings.

For Example:

If A = “aab”, 'B' = “abc”, 'C' = “aaabbc”
Here 'C' is an interleaving string of 'A' and 'B'. because 'C' contains all the characters of 'A' and 'B' and the order of all these characters is also the same in all three strings.

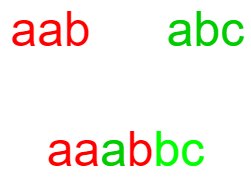
If 'A' = “abc”, 'B' = “def”, 'C' = “abcdefg”
Here 'C' is not an interleaving string of 'A' and 'B'. 'B'ecause neither A nor 'B' contains the character ‘g’.