Frontend Developer

There is a directed graph consisting of ‘N’ nodes numbered from 0 to ‘N’-1. You are given a list ‘EDGES’ of size ‘M’, consisting of all the edges of this directed graph, and two nodes ‘SRC’ and ‘DEST’ of this graph. Determine whether or not all paths starting from node ‘SRC’ eventually end at node ‘DEST’, that is -:

1. At least one path exists from node ‘SRC’ to node ‘DEST’.

2. If there exists a path from the node ‘SRC’ to a node with no outgoing edges, then that node must be ‘DEST’.

3. There should be a finite number of paths from ‘SRC’ to ‘DEST’.

You should return True if all paths starting from node ‘SRC’ eventually end at node ‘DEST’, Otherwise, return False. See the example for more clarity.

Note :

1. The given graph may have self-loops and parallel edges.

Example :

Consider ‘N’ = 4, ‘EDGES’ = [[0, 1], [0, 3], [1, 2], [3, 2]],  ‘SRC’ = 0 and ‘DEST’ = 2. The given directed graph is shown below.

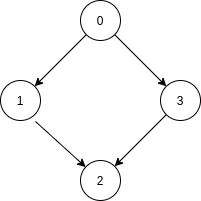
Here, all the paths that start from node 0 are -:
1. 0->1->2
2. 0->3->2
Both of these paths eventually end at node ‘2’ i.e node ‘DEST’. Thus we should return True.

I was given a wireframe of a dashboard and was asked to create a similar-looking dashboard using Angular and Node.js.

Given two numbers represented by linked lists. Your task is find the sum list and return the head of the sum list.

The sum list is a linked list representation of addition of two numbers.

You are given a linked list containing 'n' 'head' nodes, where every node in the linked list contains two pointers:

(1) ‘next’ which points to the next node in the list

(2) ‘child’ pointer to a linked list where the current node is the head.

Each of these child linked lists is in sorted order and connected by 'child' pointer.

Your task is to flatten this linked such that all nodes appear in a single layer or level in a 'sorted order'.

Input: Given linked list is:

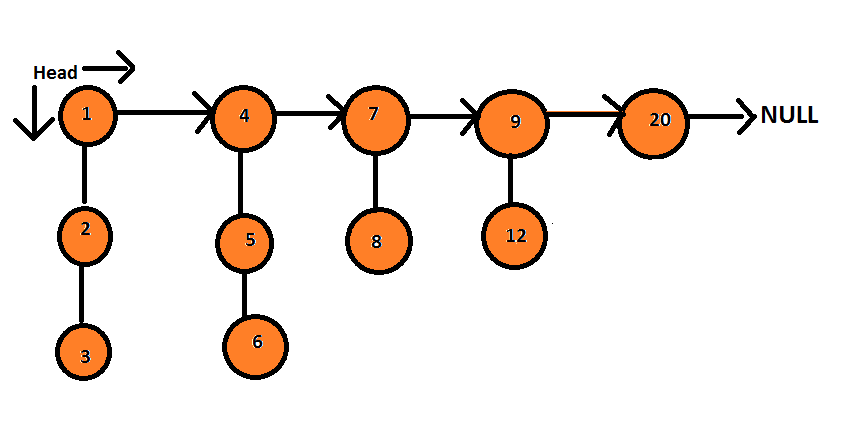
Output:
1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 12 → 20 → null.


Explanation:
The returned linked list should be in a sorted order. All the elements in this returned linked list are connected by 'child' pointers and 'next' pointers point to null.

You are given an array “ARR” of N integers. You are required to perform an operation on the array each time until it becomes empty. The operation is to select an element from the array(let’s say at ith index i.e ARR[i]) and remove one occurrence of the selected element from the array and remove all the occurrences of (ARR[i]-1) and (ARR[i]+1) from the array(if present). Your task is to maximize the sum of selected elements from the array.

For example, let’s say the given array is [2, 3, 3, 3, 4, 5].

The maximum possible sum for the given array would be 14. Because if we select one of the 3’s from the array, then one 3 and all occurrences of (3-1) and (3+1) i.e 2 and 4 will be deleted from the array. Now we left with {3,3,5} elements in the array. Then again we select 3 in the next two steps and in both steps 3 will be deleted also (3-1) and (3+1) doesn't exist in the array so nothing extra to delete in both steps. Now we left with only {5} and in the next step, we select the 5 and delete it. Then the array becomes empty. Thus the sum of selected elements will be 3+3+3+5 = 14.

Implement a Stack Data Structure specifically to store integer data using two Queues.

There should be two data members, both being Queues to store the data internally. You may use the inbuilt Queue.

Implement the following public functions :

1. Constructor:
It initializes the data members(queues) as required.

2. push(data) :
This function should take one argument of type integer. It pushes the element into the stack and returns nothing.

3. pop() :
It pops the element from the top of the stack and, in turn, returns the element being popped or deleted. In case the stack is empty, it returns -1.

4. top :
It returns the element being kept at the top of the stack. In case the stack is empty, it returns -1.

5. size() :
It returns the size of the stack at any given instance of time.

6. isEmpty() :
It returns a boolean value indicating whether the stack is empty or not.

Operations Performed on the Stack:

Query-1(Denoted by an integer 1): Pushes an integer data to the stack. (push function)

Query-2(Denoted by an integer 2): Pops the data kept at the top of the stack and returns it to the caller. (pop function)

Query-3(Denoted by an integer 3): Fetches and returns the data being kept at the top of the stack but doesn't remove it, unlike the pop function. (top function)

Query-4(Denoted by an integer 4): Returns the current size of the stack. (size function)

Query-5(Denoted by an integer 5): Returns a boolean value denoting whether the stack is empty or not. (isEmpty function)

Example

Operations: 
1 5
1 10
2
3
4

Enqueue operation 1 5: We insert 5 at the back of the queue.
  Queue: [5]

Enqueue operation 1 10: We insert 10 at the back of the queue.
  Queue: [5, 10]

Dequeue operation 2: We remove the element from the front of the queue, which is 5, and print it.
  Output: 5
  Queue: [10]

Peek operation 3: We return the element present at the front of the queue, which is 10, without removing it.
  Output: 10
  Queue: [10]

IsEmpty operation 4: We check if the queue is empty.
  Output: False
  Queue: [10]