Associate Professional

Given a sequence of ‘N’ space-separated non-negative integers A[1],A[2],A[3],......A[i]…...A[n]. Where each number of the sequence represents the height of the line drawn at point 'i'. Hence on the cartesian plane, each line is drawn from coordinate ('i',0) to coordinate ('i', 'A[i]'), here ‘i’ ranges from 1 to ‘N’. Find two lines, which, together with the x-axis forms a container, such that the container contains the most area of water.

Note :

1. You can not slant the container i.e. the height of the water is equal to the minimum height of the two lines which define the container.

2. Do not print anything, you just need to return the area of the container with maximum water.

Example

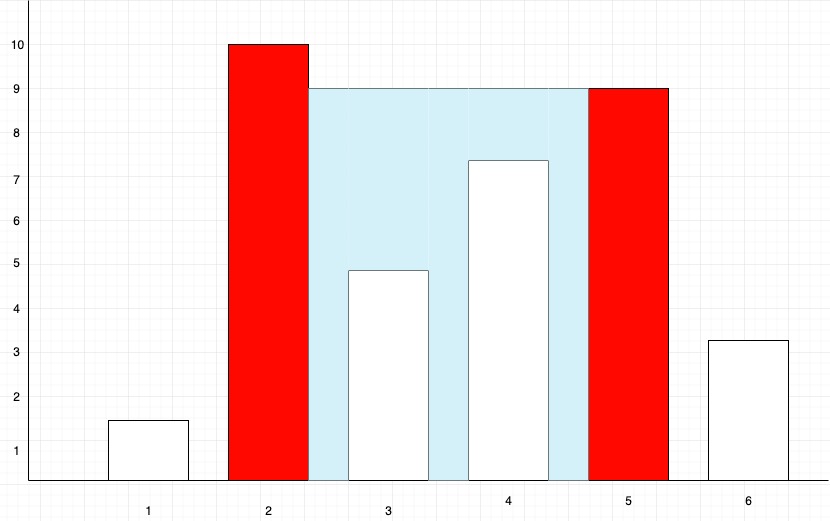
For the above Diagram, the first red marked line is formed between coordinates (2,0) and (2,10), and the second red-marked line is formed between coordinates (5,0) and (5,9). The area of water contained between these two lines is (height* width) = (5-2)* 9 = 27, which is the maximum area contained between any two lines present on the plane. So in this case, we will return 3* 9=27.

You have been given a non-empty grid consisting of only 0s and 1s. You have to find the number of islands in the given grid.

An island is a group of 1s (representing land) connected horizontally, vertically or diagonally. You can assume that all four edges of the grid are surrounded by 0s (representing water).

Regarding image processing