Mathworks interview experience Real time questions & tips from candidates to crack your interview
SDE - 2
Mathworks
6 rounds | 10 Coding
problems
Interview preparation journey
Preparation
Duration: 3 months
Topics: Data Structures, Algorithms, OOPs, System design, Operating systems
Tip
Tip 1 : Try to complete at least 2 easy, 2 medium and 1 hard problem everyday
Tip 2 : Do practice in the online coding platforms
Tip 3 : Practice as many problems as possible from topics like trees, tries, stack, queues, dp or greedy algorithms
Application process
Where: Other
Eligibility: 5 years of experience
Resume tip
Tip 1 : Make sure to specify your skills and your level of expertise in them
Tip 2 : Try to participate in some challenges/competitions, the more experience you have of solving problems/ working on nice projects, the more benefit you'll get.
Tip 3 : If you are applying for a little senior position, then team lead/management or time management this kind of extra curriculum will help.
Interview rounds
01
Round
Hard
Assignment
Duration3 days
Interview date18 Oct 2019
Coding problem1
1. Duplicate Subtrees
Moderate
30m average time
70% success
0/80
Asked in companies



You have been given a binary tree, you are supposed to return the root values of all the duplicate subtrees. For each duplicate subtree, you only need to return the root value of any one of them.
Two subtrees are duplicate if and only if they have the same structure with the same node values.
For example:
In the below binary tree :
The duplicate subtrees are {{2, 3}, {3}} and we have to just return the root values of each duplicate subtree, so the output is {2, 3}.
Problem approach
Tip 1 : How can we find duplicate subtrees in a single tree? Try to generalize the problem
Tip 2 : How to find maximum common subtrees given two trees?
02
Round
Hard
Telephonic
Duration60 Minutes
Interview date17 Oct 2019
Coding problem2
In this round I was asked 2 questions from data structures. One is basically the extension of the other. It was done during office hours itself with google docs. The interviewer was very polite and helpful. Because the question was new to me, I was trying to break down the question to smaller chunks. Al tough he didn't help me in breaking them, but after each successful step he was giving me affirmative replies which build my confidence.
1. Evaluate Expression Tree
Moderate
10m average time
90% success
0/80
Asked in companies


You are given an expression tree, your task is to evaluate the expression.
An expression tree is a binary tree where leaf nodes are integer values and internal nodes are mathematical operations.
A binary tree is a tree where every node has at most two child nodes.
Note:
There can be 4 operators: +,-,*,/. For division, you need to return the floor(a/b).
For example:
Consider the following expression tree:
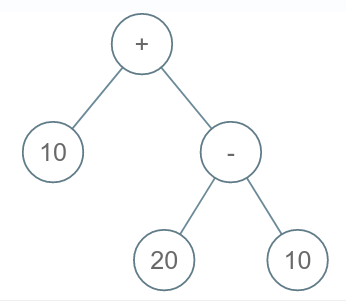
While evaluating the expression tree we replace the value at a node with any operation OP by evaluating LEFTCHILD (OP) RIGHTCHILD
Here, the expression will be evaluated as 20 - 10 = 10 (FOR ‘-’), then ‘-’ will be replaced by 10 (symbolic), then we evaluate for node’+’, 10 + 10 = 20.
2. Build Binary Expression Tree From Infix Expression
Moderate
15m average time
85% success
0/80
Asked in companies


You are given a string ‘S’, an infix expression that has operands, operators and parentheses ‘(‘ and ‘)’.
You need to return the binary expression tree, whose inorder traversal is the same as ‘S’.
Note:
Infix expression: The expression of the form ‘a operator b’. When an operator is in-between every pair of operands.
The expression tree is a binary tree in which each internal node corresponds to the operator and each leaf node corresponds to the operand so for example expression tree for 5 * ( 6 - 3 ) / 2 - 8 would be:
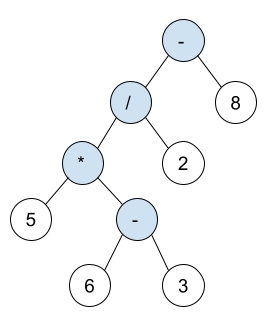
03
Round
Medium
Online Coding Interview
Duration60 Minutes
Interview date24 Oct 2019
Coding problem3
It was done in office hours only with the similar environment like last round, but with a different interviewer.
1. Intersection of Linked Lists
Easy
20m average time
70% success
0/40
Asked in companies



You are given two linked lists L1 and L2 which are sorted in ascending order. You have to make a linked list with the elements which are present in both the linked lists and are present in ascending order.
Example:-
L1 = 1->2->3->4->7
L2 = 2->4->6->7
ANSWER:- The answer should be 2->4->7 because 2,4, and 7 are present in both the linked lists.
Problem approach
1. Get count of the nodes in the lists, let counts be c1 and c2
2. Get the difference of counts d = abs(c1 – c2)
3. Now traverse the bigger list from the first node till d nodes so that from here onwards both the lists have equal no of nodes
4. Then we can traverse both the lists in parallel till we come across a common node.
2. Vertical Order Traversal
Moderate
35m average time
65% success
0/80
Asked in companies



The Ultimate Ninja Ankush is a straightforward, no-nonsense guy and loves binary Trees, and he has given you a binary tree, and you have to return the vertical order traversal of the values of the nodes of the given tree.
For each node at position (‘X’, ‘Y’), (‘X’-1, ‘Y’-1) will be its left child position while (‘X’+1, ‘Y’-1) will be the right child position.
Running a vertical line from X = -infinity to X = +infinity, now whenever this vertical line touches some nodes, we need to add those values of the nodes in order starting from top to bottom with the decreasing ‘Y’ coordinates.
Print the vertical order of the tree, to make the Ultimate Ninja Happy.
Note:
If two nodes have the same position, then the value of the node that is added first will be the value that is on the left side.
For example:
For the binary tree in the image below.
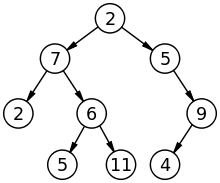
The vertical order traversal will be {2, 7, 5, 2, 6, 5, 11, 4, 9}.
Problem approach
1. We can do preorder traversal of the given Binary Tree. While traversing the tree, we can recursively calculate horizontal distances.
2. We initially pass the horizontal distance as 0 for root. For left subtree, we pass the Horizontal Distance as Horizontal distance of root minus 3. For right subtree, we pass the Horizontal Distance as Horizontal Distance of root plus 1.
3. Implement Trie
Hard
41m average time
0/120
Asked in companies



Implement Trie Data Structure to support these operations:
insert(word) - To insert a string "word" in Trie
search(word) - To check if string "word" is present in Trie or not.
startsWith(word) - To check if there is any string in the Trie that starts with the given prefix string "word".
Three type of queries denote these operations:
Type 1: To insert a string "word" in Trie.
1 word
Type 2: To check if the string "word" is present in Trie or not.
2 word
Type 3: To check if there is any string in the Trie that starts with the given prefix string "word".
3 word
Problem approach
1. Created a trie for the english dictionary. The struct with 26-childrens which looks like this-
struct TrieNode
{
struct TrieNode *children[26];
bool isEndOfWord;
};
Then implemented insert, search and delete operations for this trie.
04
Round
Medium
Video Call
Duration30 minutes
Interview date5 Nov 2019
Coding problem2
This round was with my senior manager. Where he asked me some graph related questions which might be relevant for the project that I will be working on.
1. N-th Fibonacci Number
Moderate
40m average time
70% success
0/80
Asked in companies



You are given an integer ‘N’, your task is to find and return the N’th Fibonacci number using matrix exponentiation.
Since the answer can be very large, return the answer modulo 10^9 +7.
Fibonacci number is calculated using the following formula:
F(n) = F(n-1) + F(n-2),
Where, F(1) = F(2) = 1.
For Example:
For ‘N’ = 5, the output will be 5.
Problem approach
1. First I solved using recursion. Then he asked me about the time and space complexity and if I can optimize that.
2. So I used, this formula to compute the n-th number- f[i] = f[i - 1] + f[i - 2];
3. He asked me to furthur optimize, as I was storing all n-terms here.
4. So finally I used just two variables and one for loop to solve this.
2. Aptitude Question
Is there any repeating pattern in the graph given?
How to find those patterns?
05
Round
Easy
Group Discussion
Duration15 minutes
Interview date5 Nov 2019
Coding problem1
In this round, I had to create a presentation about my education, achievements, experience so far and extra curriculum activity, etc, and present that to all my teammates. While creating this presentation, I was continuously in touch with the manager and he told me all the possible changes that he wants to see in the presentation. I think, this round they do this to check the synchronization and understanding between me and my manager.
1. Group Discussion
Education background, and project discussion among all the present members?
06
Round
Easy
HR Round
Duration20 Minutes
Interview date5 Nov 2019
Coding problem1
1. Basic HR Questions
Why do you want to join Mathworks?
What are your strengths and weaknesses?
How will you react to a conflict between you and your boss?

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
3 rounds | 4 problems
Interviewed by Mathworks
1281 views
0 comments
0 upvotes
EDG Associate
5 rounds | 4 problems
Interviewed by Mathworks
1266 views
0 comments
0 upvotes
SDE - Intern
1 rounds | 3 problems
Interviewed by Amazon
3407 views
0 comments
0 upvotes
EDG Engineer
4 rounds | 7 problems
Interviewed by Mathworks
396 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 2
5 rounds | 12 problems
Interviewed by Walmart
29739 views
8 comments
0 upvotes
SDE - 2
3 rounds | 5 problems
Interviewed by Amazon
6728 views
1 comments
0 upvotes
SDE - 2
6 rounds | 8 problems
Interviewed by Amazon
5225 views
0 comments
0 upvotes






