SDE - 1

Given an array/list of integer numbers 'CHOCOLATES' of size 'N', where each value of the array/list represents the number of chocolates in the packet. There are ‘M’ number of students and the task is to distribute the chocolate to their students. Distribute chocolate in such a way that:

1. Each student gets at least one packet of chocolate.

2. The difference between the maximum number of chocolate in a packet and the minimum number of chocolate in a packet given to the students is minimum.

Example :

Given 'N' : 5 (number of packets) and 'M' : 3 (number of students)

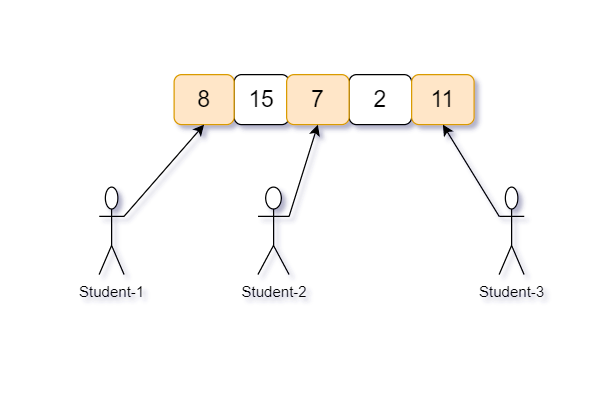
And chocolates in each packet is : {8, 11, 7, 15, 2}

All possible way to distribute 5 packets of chocolates among 3 students are -

( 8,15, 7 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 8, 15, 2 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’ 
( 8, 15, 11 ) difference of maximum-minimum is ‘15 - 8’ = ‘7’
( 8, 7, 2 ) difference of maximum-minimum is ‘8 - 2’ = ‘6’
( 8, 7, 11 ) difference of maximum-minimum is ‘11 - 7’ = ‘4’
( 8, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’
( 15, 7, 2 ) difference of maximum-minimum is ‘15 - 2’ = 13’
( 15, 7, 11 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 15, 2, 11 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’
( 7, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’

Hence there are 10 possible ways to distribute ‘5’ packets of chocolate among the ‘3’ students and difference of combination (8, 7, 11) is ‘maximum - minimum’ = ‘11 - 7’ = ‘4’ is minimum in all of the above.

'N' students are standing in a row. You are given the height of every student standing in the row. Your task is to find the longest strictly increasing subsequence of heights from the row such that the relative order of the students does not change.

A subsequence is a sequence that can be derived from another sequence by deleting zero or more elements without changing the order of the remaining elements.

You are given a graph with 'N' vertices numbered from '1' to 'N' and 'M' edges. You have to colour this graph in two different colours, say blue and red such that no two vertices connected by an edge are of the same colour.

Note :

The given graph may have connected components.

Given 'N' number of intervals, where each interval contains two integers denoting the boundaries of the interval. The task is to merge all the overlapping intervals and return the list of merged intervals sorted in ascending order.

Two intervals will be considered to be overlapping if the starting integer of one interval is less than or equal to the finishing integer of another interval, and greater than or equal to the starting integer of that interval.

Example:

for the given 5 intervals - [1,4], [3,5], [6,8], [10,12], [8,9].
Since intervals [1,4] and [3,5] overlap with each other, we will merge them into a single interval as [1,5].

Similarly [6,8] and [8,9] overlaps, we merge them into [6,9].

Interval [10,12] does not overlap with any interval.

Final List after merging overlapping intervals: [1,5], [6,9], [10,12]

Design a Web Crawler.