SDE - Intern

You're given a positive integer represented in the form of a singly linked-list of digits. The length of the number is 'n'.

Add 1 to the number, i.e., increment the given number by one.

The digits are stored such that the most significant digit is at the head of the linked list and the least significant digit is at the tail of the linked list.

Example:

Input: Initial Linked List: 1 -> 5 -> 2

Output: Modified Linked List: 1 -> 5 -> 3

Explanation: Initially the number is 152. After incrementing it by 1, the number becomes 153.

Aahad and Harshit always have fun by solving problems. Harshit took a sorted array consisting of distinct integers and rotated it clockwise by an unknown amount. For example, he took a sorted array = [1, 2, 3, 4, 5] and if he rotates it by 2, then the array becomes: [4, 5, 1, 2, 3].

After rotating a sorted array, Aahad needs to answer Q queries asked by Harshit, each of them is described by one integer Q[i]. which Harshit wanted him to search in the array. For each query, if he found it, he had to shout the index of the number, otherwise, he had to shout -1.

For each query, you have to complete the given method where 'key' denotes Q[i]. If the key exists in the array, return the index of the 'key', otherwise, return -1.

Note:

Can you solve each query in O(logN) ?

You have been given a grid containing some oranges. Each cell of this grid has one of the three integers values:

Value 0 - representing an empty cell.

Value 1 - representing a fresh orange.

Value 2 - representing a rotten orange.

Every second, any fresh orange that is adjacent(4-directionally) to a rotten orange becomes rotten.

Your task is to find out the minimum time after which no cell has a fresh orange. If it's impossible to rot all the fresh oranges then print -1.

Note:

1. The grid has 0-based indexing.
2. A rotten orange can affect the adjacent oranges 4 directionally i.e. Up, Down, Left, Right.

Ninjas is practicing problems on the linked list. He came across a problem in which he has given a linked list of ‘N’ nodes and two integers, ‘LOW’ and ‘HIGH’. He has to return the linked list ‘HEAD’ after reversing the nodes between ‘LOW’ and ‘HIGH’, including the nodes at positions ‘LOW’ and ‘HIGH’.

You have been given a Snake and Ladder Board with 'N' rows and 'N' columns with the numbers written from 1 to (N*N) starting from the bottom left of the board, and alternating direction each row.

For example

For a (6 x 6) board, the numbers are written as follows:

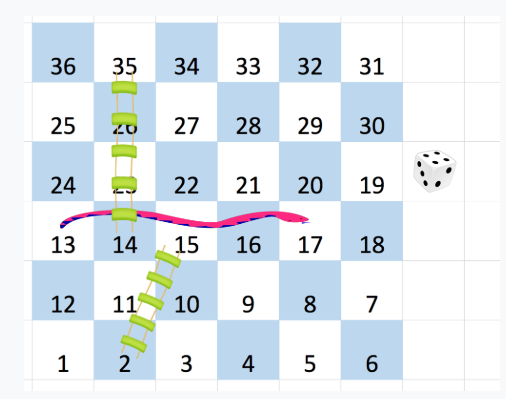
You start from square 1 of the board (which is always in the last row and first column). On each square say 'X', you can throw a dice which can have six outcomes and you have total control over the outcome of dice throw and you want to find out the minimum number of throws required to reach the last cell.
Some of the squares contain Snakes and Ladders, and these are possibilities of a throw at square 'X':
You choose a destination square 'S' with number 'X+1', 'X+2', 'X+3', 'X+4', 'X+5', or 'X+6', provided this number is <= N*N.
If 'S' has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.
A board square on row 'i' and column 'j' has a "Snake or Ladder" if board[i][j] != -1. The destination of that snake or ladder is board[i][j].

Note :

You can only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving - you have to ignore the snake or ladder present on that square.

For example, if the board is:
-1 1 -1
-1 -1 9
-1 4 -1
Let's say on the first move your destination square is 2  [at row 2, column 1], then you finish your first move at 4 [at row 1, column 2] because you do not continue moving to 9 [at row 0, column 0] by taking the ladder from 4.

A square can also have a Snake or Ladder which will end at the same cell.
For example, if the board is:
-1 3 -1
-1 5 -1
-1 -1 9
Here we can see Snake/Ladder on square 5 [at row 1, column 1] will end on the same square 5.