SDE - 1

Given a binary tree, convert this binary tree into its mirror tree.

A binary tree is a tree in which each parent node has at most two children.

Mirror of a Tree: Mirror of a Binary Tree T is another Binary Tree M(T) with left and right children of all non-leaf nodes interchanged.

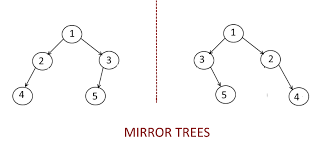
Note:

1. Make in-place changes, that is, modify the nodes given a binary tree to get the required mirror tree.

You are given a string 'S'. Your task is to partition 'S' such that every substring of the partition is a palindrome. You need to return all possible palindrome partitioning of 'S'.

Note: A substring is a contiguous segment of a string.

For Example:

For a given string “BaaB”
3 possible palindrome partitioning of the given string are:
{“B”, “a”, “a”, “B”}
{“B”, “aa”, “B”}
{“BaaB”}
Every substring of all the above partitions of “BaaB” is a palindrome.

You are given a 'Binary Tree'.

Return the bottom view of the binary tree.

Note :

1. A node will be in the bottom-view if it is the bottom-most node at its horizontal distance from the root. 

2. The horizontal distance of the root from itself is 0. The horizontal distance of the right child of the root node is 1 and the horizontal distance of the left child of the root node is -1. 

3. The horizontal distance of node 'n' from root = horizontal distance of its parent from root + 1, if node 'n' is the right child of its parent.

4. The horizontal distance of node 'n' from root = horizontal distance of its parent from the root - 1, if node 'n' is the left child of its parent.

5. If more than one node is at the same horizontal distance and is the bottom-most node for that horizontal distance, including the one which is more towards the right.

Example:

Input: Consider the given Binary Tree:

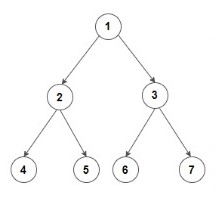
Output: 4 2 6 3 7

Explanation:
Below is the bottom view of the binary tree.

1 is the root node, so its horizontal distance = 0.
Since 2 lies to the left of 0, its horizontal distance = 0-1= -1
3 lies to the right of 0, its horizontal distance = 0+1 = 1
Similarly, horizontal distance of 4 = Horizontal distance of 2 - 1= -1-1=-2
Horizontal distance of 5 = Horizontal distance of 2 + 1=  -1+1 = 0
Horizontal distance of 6 = 1-1 =0
Horizontal distance of 7 = 1+1 = 2

The bottom-most node at a horizontal distance of -2 is 4.
The bottom-most node at a horizontal distance of -1 is 2.
The bottom-most node at a horizontal distance of 0 is 5 and 6. However, 6 is more towards the right, so 6 is included.
The bottom-most node at a horizontal distance of 1 is 3.
The bottom-most node at a horizontal distance of 2 is 7.

Hence, the bottom view would be 4 2 6 3 7

You are given two strings 'str1' and 'str1'.

You have to tell whether these strings form an anagram pair or not.

The strings form an anagram pair if the letters of one string can be rearranged to form another string.

Pre-requisites:

Anagrams are defined as words or names that can be formed by rearranging the letters of another word. Such as "spar" can be formed by rearranging letters of "rasp". Hence, "spar" and "rasp" are anagrams. 

Other examples include:

'triangle' and 'integral'
'listen' and 'silent'

Note:

Since it is a binary problem, there is no partial marking. Marks will only be awarded if you get all the test cases correct. 

You are given a binary tree consisting of 'n' nodes.

Convert the given binary tree into a linked list where the linked list nodes follow the same order as the pre-order traversal of the given binary tree.

Use the right pointer of the binary tree as the “next” pointer for the linked list and set the left pointer to NULL.

Use these nodes only. Do not create extra nodes.

Example :

Input: Let the binary be as shown in the figure:

Output: Linked List: 15 -> 40 -> 62 -> 10 -> 20 -> NULL

Explanation: As shown in the figure, the right child of every node points to the next node, while the left node points to null.

Also, the nodes are in the same order as the pre-order traversal of the binary tree.

Design a data structure that stores a mapping of a key to a given value and supports the following operations in constant time.

1. INSERT(key, value): Inserts an integer value to the data structure against a string type key if not already present. If already present, it updates the value of the key with the new one. This function will not return anything.

2. DELETE(key): Removes the key from the data structure if present. It doesn't return anything.

3. SEARCH(key): It searches for the key in the data structure. In case it is present, return true. Otherwise, return false.

4. GET(key): It returns the integer value stored against the given key. If the key is not present, return -1. 

5. GET_SIZE(): It returns an integer value denoting the size of the data structure. 

6. IS_EMPTY(): It returns a boolean value, denoting whether the data structure is empty or not. 

Note :

1. Key is always a string value.
2. Value can never be -1.

Operations Performed :

First(Denoted by integer value 1):  Insertion to the Data Structure. It is done in a pair of (key, value).

Second(Denoted by integer value 2):  Deletion of a key from the Data Structure.

Third(Denoted by integer value 3): Search a given key in the Data Structure.

Fourth(Denoted by integer value 4): Retrieve the value for a given key from the Data Structure.

Fifth(Denoted by integer value 5): Retrieve the size of the Data Structure.

Sixth(Denoted by integer value 6): Retrieve whether the Data Structure is empty or not.