SDE

Ram went to a specialty candy store in Ninjaland which has 'N' candies with different costs.

The Candy shop gives a special offer to its customers. A customer can buy a single candy from the store and get at most 'K' different candies for free. Now, Ram is interested in knowing the maximum and the minimum amount he needs to spend for buying all the candies available in the store.

Note: In both cases, Ram must utilize the offer i.e. if 'K' or more candies are available, he must take 'K' candies for every candy purchase. If less than K candies are available, he must take all candies for a candy purchase.

For Example :

For 'N' =  5 and 'K' = 2

Let the cost of different candies in the store be: [9 8 2 6 4]

For the minimum amount: 
Ram can buy a candy with cost 2 and take candies with costs 9 and 8 for free. 
Then, he can buy a candy with cost 4 and take candy with cost 7 for free. 
Thus, the minimum cost will be 6 i.e. 2 + 4. 

For the maximum amount: 
Ram can buy a candy with cost 9 and take candies with costs 2 and 6 for free. 
Then, he can buy candy at cost 8 and take candy at cost 4 for free. 
Thus, the minimum cost will be 17 i.e. 9 + 8.

Thus, Minimum = 6 and Maximum = 17.

There are ‘N’ numbers of balls in a room that are placed in a row. You are given an array ‘location’ where location[ i ] denotes the location of the ‘i-th’ ball.

You have to move all the balls at the same location, and it is given that you can move a ball from position [ i ] to

1. position[i] + 2 with cost = 0.

2. position[i] + 1 with cost = 1.

Your task is to find the minimum cost required to move all the balls at the same location.

For Example :

If we have three balls placed at [ 1, 3, 4 ]

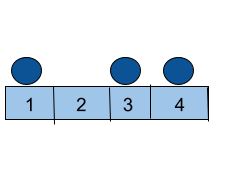
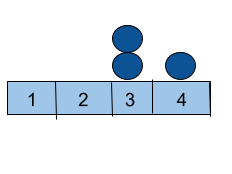
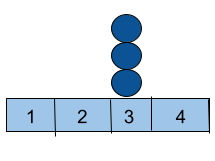
At first, move the ball from position ‘1’ to position ‘3’ with cost = 0.
Then move the ball from position ‘4’ to position ‘3’ with cost =1.
As the minimum cost = 1, so you need to print 1.

You have been given 'N' ropes of different lengths, we need to connect these ropes into one rope. The cost to connect two ropes is equal to sum of their lengths. We need to connect the ropes with minimum cost.

The test-data is such that the result will fit into a 32-bit integer.

You have been given an undirected graph with 'N' vertices and 'M' edges. The vertices are labelled from 1 to 'N'.

Your task is to find if the graph contains a cycle or not.

A path that starts from a given vertex and ends at the same vertex traversing the edges only once is called a cycle.

Example :

In the below graph, there exists a cycle between vertex 1, 2 and 3. 

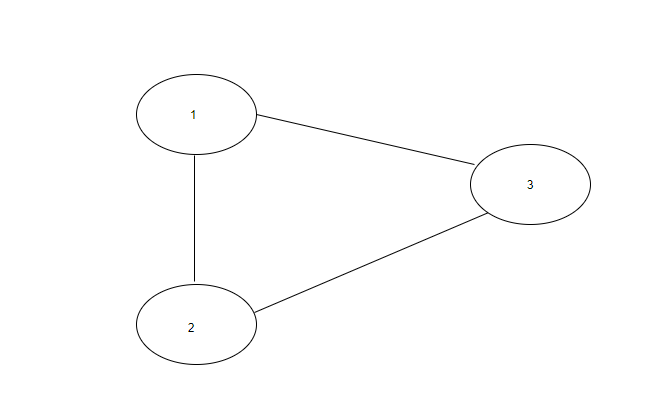
Note:

1. There are no parallel edges between two vertices.

2. There are no self-loops(an edge connecting the vertex to itself) in the graph.

3. The graph can be disconnected.

For Example :

Input: N = 3 , Edges =  [[1, 2], [2, 3], [1, 3]].
Output: Yes

Explanation : There are a total of 3 vertices in the graph. There is an edge between vertex 1 and 2, vertex 2 and 3 and vertex 1 and 3. So, there exists a cycle in the graph.