SDE - 1

You are given a 2-dimensional array/list having N rows and M columns, which is filled with ones(1) and zeroes(0). 1 signifies land, and 0 signifies water.

A cell is said to be connected to another cell, if one cell lies immediately next to the other cell, in any of the eight directions (two vertical, two horizontal, and four diagonals).

A group of connected cells having value 1 is called an island. Your task is to find the number of such islands present in the matrix.

You are having a stack "ARR" of size 'N+1', your task is to delete the middlemost element so that the size of resulting stack is 'N'.

A stack is a linear data structure where both insertion and deletion of elements take place at the top. It follows FILO (First In Last Out) or LIFO (Last In First Out) approaches. Books piled on top of each other is an example of a stack, where you can only remove a single book at a time, which is at the top of the stack. Likewise, you can only add a single book at a time, on the top of the stack only.

Example :-

INPUT : ARR [ ] = [ 1 , 2 , 3 , 4 , 5 ] , N = 4
OUTPUT: ARR [ ] = [ 1 , 2 , 4,  5 ]

The above example contains an odd number of elements, hence the middle element is clearly the (N+1) / 2th element, which is removed from the stack in the output.

INPUT : ARR [ ] = [ 5, 6, 7, 8 ] , N = 3
OUTPUT: ARR [ ] = [ 5, 7, 8 ]

The above example contains an even number of elements, so out of the two middle elements, we consider the one which occurs first. Hence, the middle element would be ((N+1) / 2 - 1) element, which is 6 and is removed from the stack in the output.

You are given an array 'ARR' of 'N' distinct integers.

Your task is to find the product 'P' with the highest count('C') of quadruples which follow p * q = r * s where p, q, r, and s are elements of the array with different indexes.

Note:

1. Quadruple p*q = r*s is the same as r*s = p*q.

2. If 2 or more products have the same count of quadruples, print the lowest value of the product i.e if (P1, P2) are the 2 products with the same count of such quadruples(C1 = C2) then 'P' = min(P1, P2).

3. If no such quadruple exists('C' = 0), return 0.

Example:

If the given array is [3, 4, 6, 2, 1], then the answer would be 6 1. Because there are two products 'P' i.e 6 and 12 which have the highest and same count 'C' of quadruples, i.e 'C' = 1. Therefore the lowest value of the product 'P' is the answer i.e 6.

You have been given a Snake and Ladder Board with 'N' rows and 'N' columns with the numbers written from 1 to (N*N) starting from the bottom left of the board, and alternating direction each row.

For example

For a (6 x 6) board, the numbers are written as follows:

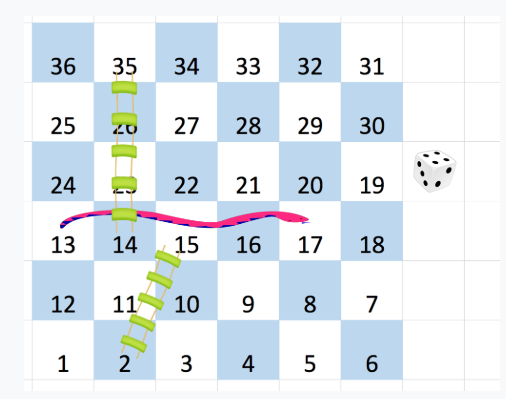
You start from square 1 of the board (which is always in the last row and first column). On each square say 'X', you can throw a dice which can have six outcomes and you have total control over the outcome of dice throw and you want to find out the minimum number of throws required to reach the last cell.
Some of the squares contain Snakes and Ladders, and these are possibilities of a throw at square 'X':
You choose a destination square 'S' with number 'X+1', 'X+2', 'X+3', 'X+4', 'X+5', or 'X+6', provided this number is <= N*N.
If 'S' has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.
A board square on row 'i' and column 'j' has a "Snake or Ladder" if board[i][j] != -1. The destination of that snake or ladder is board[i][j].

Note :

You can only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving - you have to ignore the snake or ladder present on that square.

For example, if the board is:
-1 1 -1
-1 -1 9
-1 4 -1
Let's say on the first move your destination square is 2  [at row 2, column 1], then you finish your first move at 4 [at row 1, column 2] because you do not continue moving to 9 [at row 0, column 0] by taking the ladder from 4.

A square can also have a Snake or Ladder which will end at the same cell.
For example, if the board is:
-1 3 -1
-1 5 -1
-1 -1 9
Here we can see Snake/Ladder on square 5 [at row 1, column 1] will end on the same square 5.