SDE - 1

You are given an array Arr consisting of N integers. You need to find the equilibrium index of the array.

An index is considered as an equilibrium index if the sum of elements of the array to the left of that index is equal to the sum of elements to the right of it.

Note:

1. The array follows 0-based indexing, so you need to return the 0-based index of the element.
2. Note that the element at the equilibrium index won’t be considered for either left sum or right sum.
3. If there are multiple indices which satisfy the given condition, then return the left-most index i.e if there are indices i,j,k…. which are equilibrium indices, return the minimum among them
4. If no such index is present in the array, return -1.

You are given a 'Binary Tree'.

Return the bottom view of the binary tree.

Note :

1. A node will be in the bottom-view if it is the bottom-most node at its horizontal distance from the root. 

2. The horizontal distance of the root from itself is 0. The horizontal distance of the right child of the root node is 1 and the horizontal distance of the left child of the root node is -1. 

3. The horizontal distance of node 'n' from root = horizontal distance of its parent from root + 1, if node 'n' is the right child of its parent.

4. The horizontal distance of node 'n' from root = horizontal distance of its parent from the root - 1, if node 'n' is the left child of its parent.

5. If more than one node is at the same horizontal distance and is the bottom-most node for that horizontal distance, including the one which is more towards the right.

Example:

Input: Consider the given Binary Tree:

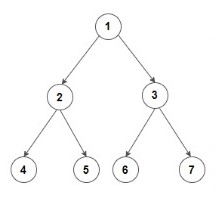
Output: 4 2 6 3 7

Explanation:
Below is the bottom view of the binary tree.

1 is the root node, so its horizontal distance = 0.
Since 2 lies to the left of 0, its horizontal distance = 0-1= -1
3 lies to the right of 0, its horizontal distance = 0+1 = 1
Similarly, horizontal distance of 4 = Horizontal distance of 2 - 1= -1-1=-2
Horizontal distance of 5 = Horizontal distance of 2 + 1=  -1+1 = 0
Horizontal distance of 6 = 1-1 =0
Horizontal distance of 7 = 1+1 = 2

The bottom-most node at a horizontal distance of -2 is 4.
The bottom-most node at a horizontal distance of -1 is 2.
The bottom-most node at a horizontal distance of 0 is 5 and 6. However, 6 is more towards the right, so 6 is included.
The bottom-most node at a horizontal distance of 1 is 3.
The bottom-most node at a horizontal distance of 2 is 7.

Hence, the bottom view would be 4 2 6 3 7

You are given a string 'str' of length 'N'. You can perform at most 'k' operations on this string. In one operation, you can choose any character of the string and change it to any other uppercase English alphabet character.

Return the length of the longest substring containing same characters after performing the above operations.

For example :

Input:
str="AABC"  k=1

Output:3

Explanation: Replace 'B' with 'A', we will get "AAAC" and the longest substring with same character is "AAA" of length 3.

You are given two strings, 'str1' and 'str2'. You have to find the length of the longest common substring.

A substring is a continuous segment of a string. For example, "bcd" is a substring of "abcd", while "acd" or "cda" are not.

Example:

Input: ‘str1’ = “abcjklp” , ‘str2’ = “acjkp”.

Output: 3

Explanation:  The longest common substring between ‘str1’ and ‘str2’ is “cjk”, of length 3.

There are 100 doors in a row, and all doors are initially closed. A person walks through all the doors multiple times and toggles (if a door is open, then close it; if it is closed, then open it) them in the following way:

In the first walk, the person toggles every door.

In the second walk, the person toggles every second door, i.e., the 2nd, 4th, 6th, 8th, etc.

In the third walk, the person toggles every third door, i.e., the 3rd, 6th, 9th, etc.

Likewise,

In the 100th walk, the person toggles the 100th door.

Which doors are open in the end?

In a one-day, international cricket match, considering no extras (no wides, no ‘no’ balls, etc.) and no overthrows.

What is the maximum number of runs that a batsman can score in an ideal case?

Given 'N' number of intervals, where each interval contains two integers denoting the boundaries of the interval. The task is to merge all the overlapping intervals and return the list of merged intervals sorted in ascending order.

Two intervals will be considered to be overlapping if the starting integer of one interval is less than or equal to the finishing integer of another interval, and greater than or equal to the starting integer of that interval.

Example:

for the given 5 intervals - [1,4], [3,5], [6,8], [10,12], [8,9].
Since intervals [1,4] and [3,5] overlap with each other, we will merge them into a single interval as [1,5].

Similarly [6,8] and [8,9] overlaps, we merge them into [6,9].

Interval [10,12] does not overlap with any interval.

Final List after merging overlapping intervals: [1,5], [6,9], [10,12]