Rootstock Software interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Rootstock Software
2 rounds | 4 Coding
problems
Interview preparation journey
Journey
I started my coding journey on youtube, where I first learned the data structure and Algorithm. Then I started my preparation of Data Structure on websites.
Application story
I applied through referral from a senior. .
Why selected/rejected for the role?
I was rejected because I could not give precise and optimized solutions to the questions asked.
Preparation
Duration: 4 months
Topics: Data Structures, Pointers, OOPS, System Design, Algorithms, Dynamic Programming,System Design, Link List and Graphs
Tip
Tip 1 : Practice at least 250 coding questions
Tip 2 : Do at least two projects
Application process
Where: Referral
Eligibility: Above 6 CGPA
Resume tip
Tip 1 : Have some projects on resume.
Tip 2 : Do not put false things on resume
Interview rounds
01
Round
Easy
Video Call
Duration45 minutes
Interview date29 Jun 2023
Coding problem2
1. Check If Linked List Is Palindrome
Easy
15m average time
85% success
0/40
Asked in companies



You are given a Singly Linked List of integers. You have to return true if the linked list is palindrome, else return false.
A Linked List is a palindrome if it reads the same from left to right and from right to left.
Example:
The lists (1 -> 2 -> 1), (3 -> 4 -> 4-> 3), and (1) are palindromes, while the lists (1 -> 2 -> 3) and (3 -> 4) are not.
2. Distinct Subsequences
Moderate
10m average time
80% success
0/80
Asked in companies



You have been given string 'S' of length 'N' that may contain duplicate alphabets. Your task is to return the count of distinct subsequences of it.
For example:
For the given string “deed” :
The possible subsequences are {“”}, {“d”}, {“e”}, {“de”}, {“e”}, {“de”}, {“ee”}, {“dee”}, {“d”}, {“dd”}, {“ed”}, {“ded”}, {“ed”}, {“ded”}, {“eed”} and {“deed”}.
As, {“d”}, {“e”}, {“de”}, {“ed”} and {“ded”} are repeated.
The distinct subsequences are {“”}, {“d”}, {“e”}, {“de”}, {“ee”}, {“dee”}, {“dd”}, {“ed”}, {“ded”}, {“eed”} and {“deed”}
Thus, the output will be 11.
Note:
As the answer can be large, return your answer modulo 10^9 + 7.
Problem approach
First create a queue of pair and push only those elements in the queue which is rotten, after that run while loop until queue is empty and pop elements and push nearby elements which is not rotten and make them rotten.
02
Round
Easy
Video Call
Duration45 minutes
Interview date29 Jun 2023
Coding problem2
1. Reverse Linked List
Moderate
15m average time
85% success
0/80
Asked in companies



Given a singly linked list of integers. Your task is to return the head of the reversed linked list.
For example:
The given linked list is 1 -> 2 -> 3 -> 4-> NULL. Then the reverse linked list is 4 -> 3 -> 2 -> 1 -> NULL and the head of the reversed linked list will be 4.
Follow Up :
Can you solve this problem in O(N) time and O(1) space complexity?
Problem approach
Initialize three pointers prev as NULL, curr as head, and next as NULL.
Iterate through the linked list. In a loop, do the following:
Before changing the next of curr, store the next node
next = curr -> next
Now update the next pointer of curr to the prev
curr -> next = prev
Update prev as curr and curr as next
prev = curr
curr = next
2. Is SubSequence
Easy
10m average time
90% success
0/40
Asked in companies



You have been given two strings ‘STR1’ and ‘STR2’.
Your task is to find if ‘STR1’ is a subsequence of ‘STR2’.
A subsequence of a string is a new string that can be derived from the original string by deleting some characters (can be none) without changing the relative ordering of other characters.
Example:
‘ACE’ is a subsequence of ‘ABCDE’ because ‘ACE’ can be formed by deleting ‘B’ and ‘D’ without changing the relative order of characters. ‘ADB’ is not a subsequence of ‘ABCDE’ because we can get ‘ABD’ from ‘ABCDE’ but not ‘ADB’ and in ‘ADB’ relative order of ‘B’ and ‘D’ are different from original strings.
Note:
1.Strings ‘STR1’ and ‘STR2’ consists only of English uppercases.
2.Length of string ‘STR2’ will always be greater than or equal to the length of string ‘STR1’.
Example:
For example, the given ‘STR1’ is ‘BAE’ and ‘STR2’ is ‘ABADE’.
String ‘STR1’ is a subsequence of string ‘STR2’ because ‘BAE’ can be formed by deleting ‘A’ and ‘D’ from ‘ABADE’ and the relative ordering of the characters of the string ‘ABADE’ persists.
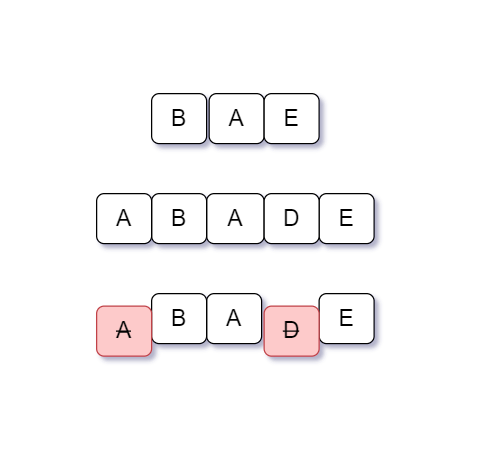
Problem approach
Run from end of both strings and each time if s[i]==t[j] then i-- and j-- and if s[i]!=t[j] then j--. If in the end i comes to be -1 it means whole string is found in sequence in t

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
3 rounds | 6 problems
Interviewed by Rootstock Software
772 views
0 comments
0 upvotes
SDE - 1
3 rounds | 6 problems
Interviewed by Rootstock Software
686 views
0 comments
0 upvotes
SDE - 1
3 rounds | 5 problems
Interviewed by Rootstock Software
691 views
0 comments
0 upvotes
Software Developer
3 rounds | 5 problems
Interviewed by Rootstock Software
969 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114869 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58031 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35057 views
7 comments
0 upvotes




