SDE - Intern

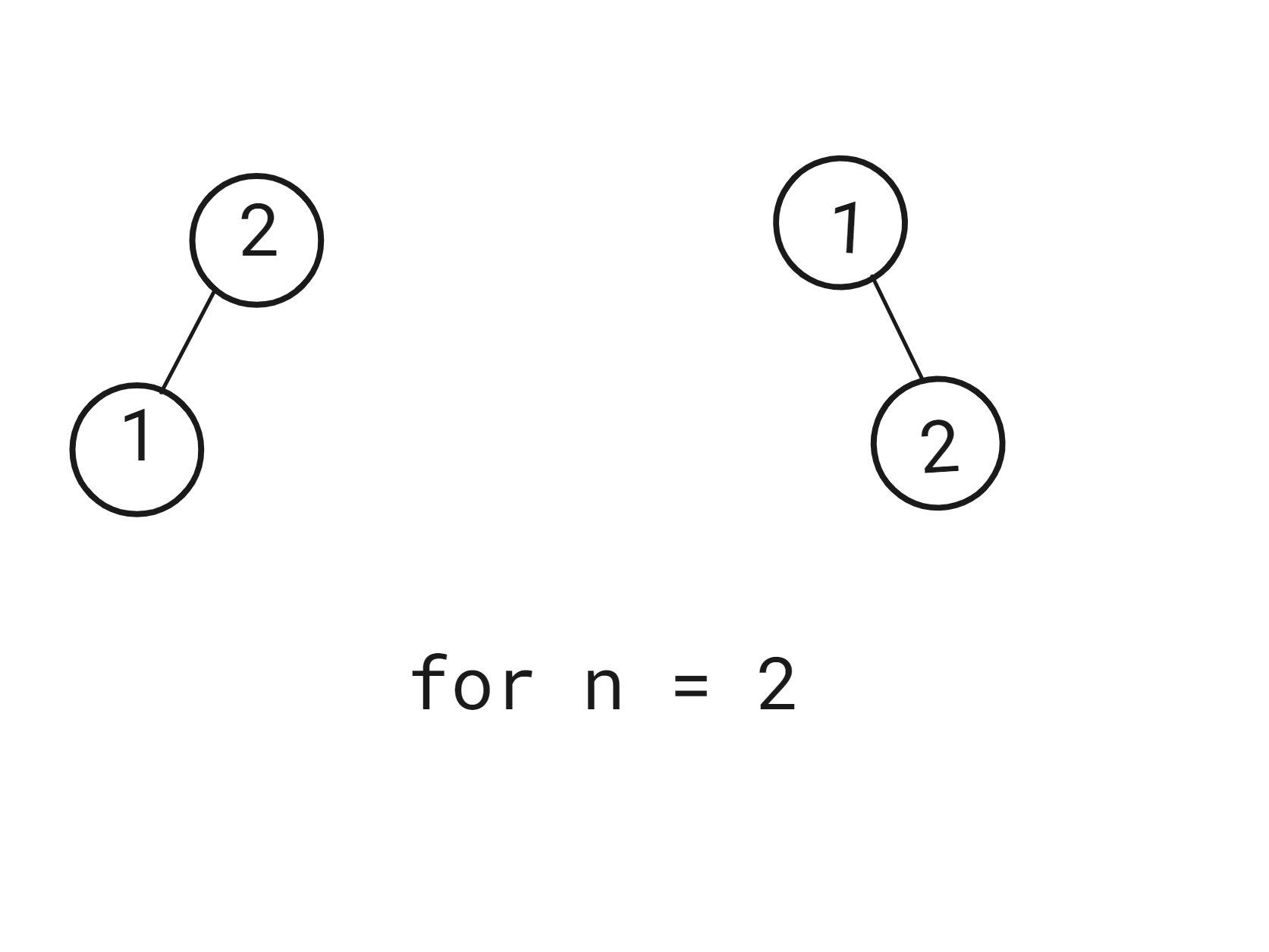
You are given an integer ‘N’, your task is to return the number of structurally unique BST's (binary search trees) which have exactly 'N' nodes of unique values from 1 to 'N'.

For example:

Given  ‘N’ = 2, The total number of BST’s is 2.

Note:

1. A binary search tree is a rooted binary tree whose internal nodes each store a key greater than all the keys in the node's left subtree and less than those in its right subtree.

2. A structurally unique binary search tree is a tree that has at least 1 node at a different position or with a different value compared to another binary search tree.

You are given an arbitrary array ‘arr’ consisting of N non-negative integers, where every element appears thrice except one. You need to find the element that appears only once.

You are given a binary tree consisting of ‘N’ nodes. Your task is to replace all the half nodes present in the binary tree with its child node. Half nodes are those nodes that have only one child.

For Example:

In this given binary tree, nodes 7, 5, and 9 are half nodes because they have only one child node. So we have to replace these nodes with their child. The inorder traversal of the updated binary tree is [1, 6, 11, 2, 4]. Hence, the answer is [1, 6, 11, 2, 4].

Example:

Elements are in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1

Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. 

The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (-1).

Note :

The above format was just to provide clarity on how the input is formed for a given tree. 

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1