Software Developer

A thief is robbing a store and can carry a maximum weight of ‘W’ into his knapsack. There are 'N' items available in the store and the weight and value of each item is known to the thief. Considering the constraints of the maximum weight that a knapsack can carry, you have to find the maximum profit that a thief can generate by stealing items.

Note: The thief is not allowed to break the items.

For example, N = 4, W = 10 and the weights and values of items are weights = [6, 1, 5, 3] and values = [3, 6, 1, 4]. Then the best way to fill the knapsack is to choose items with weight 6, 1 and 3. The total value of knapsack = 3 + 6 + 4 = 13.

Given two strings ‘STR’ and ‘PTR’. Find all the starting indices of ‘PTR’ anagram substring in ‘STR’. Two strings are anagram if and only if one string can be converted into another string by rearranging the character.

For example, ‘ABCD’ and ‘ACBD’ are two anagram strings because ‘ACBD’ can be converted into ‘ABCD’ by rearranging the ‘B’ and ‘C’. ’ABA’ and ‘ABB’ are not anagram because we can’t convert ‘ABA’ to ‘ABB’ by rearranging the characters of particular strings.

‘ABACD’ and ‘CABAD’ are anagram because ‘ABACD’ can be converted into ‘CABAD’ by rearranging the first ‘A’ with ‘C’ and second ‘A’ with ‘B’.

Note:

Strings ‘STR’ and ‘PTR’ consist only of English uppercases.

Length of string ‘STR’ will always be greater than or equal to the length of string ‘PTR’.

The index is ‘0’ based.

In case, there is no anagram substring then return an empty sequence.

Explanation:

For example, the given ‘STR’ is ‘BACDGABCD’ and ‘PTR’ is ‘ABCD’. Indices are given

0-3 in ‘STR’ index 0,1,2,3 are ‘BACD’ and it is an anagram with ‘ABCD’
1-4 in ‘STR’ index 1,2,3,4 are ‘ACDG’ and it is not anagram with ‘ABCD’
2-5 in ‘STR’ index 2,3,4,5 are ‘CDGA’ and it is not anagram with ‘ABCD’
3-6 in ‘STR’ index 3,4,5,6 are ‘DGAB’ and it is not anagram with ‘ABCD’
4-7 in ‘STR’ index 4,5,6,7 are ‘GABC’ and it is not anagram with ‘ABCD’
5-8 in ‘STR’ index 5,6,7,8 are ‘ABCD’ and it is an anagram with ‘ABCD’

Hence there are 2 starting indices of substrings in the string ‘STR’ that are anagram with given ‘PTR’  which are index 0 and 5.

You have been given a Binary Tree of 'N' nodes, where the nodes have integer values. Your task is to print the zigzag traversal of the given tree.

Note:

In zigzag order, level 1 is printed from left to right fashion, level 2 is printed from right to left. and level 3 is printed from left to right again, and so on…..

For example:

For the given binary tree

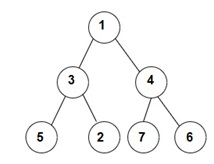
The zigzag  traversal is [1, 4, 3, 5, 2, 7, 6]

You have been given an integer array/list (ARR) of size N. You have to return an array/list PRODUCT such that PRODUCT[i] is equal to the product of all the elements of ARR except ARR[i]

 Note :

Each product can cross the integer limits, so we should take modulo of the operation. 

Take MOD = 10^9 + 7 to always stay in the limits.

Follow up :

Can you try solving the problem in O(1) space?

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

1. Push(num): Push the given number in the stack.
2. Pop: Remove and return the top element from the stack if present, else return -1.
3. Top: return the top element of the stack if present, else return -1.
4. getMin: Returns minimum element of the stack if present, else return -1.

For Example:

For the following input: 
1
5
1 1
1 2
4
2
3

For the first two operations, we will just insert 1 and then 2 into the stack which was empty earlier. So now the stack is => [2,1]
In the third operation, we need to return the minimum element of the stack, i.e., 1. So now the stack is => [2,1]
For the fourth operation, we need to pop the topmost element of the stack, i.e., 2. Now the stack is => [1]
In the fifth operation, we return the top element of the stack, i.e. 1 as it has one element. Now the stack is => [1]

So, the final output will be: 
1 2 1

You are given a Singly Linked List of integers. Return true if it has a cycle, else return false.

A cycle occurs when a node's next points back to a previous node in the list.

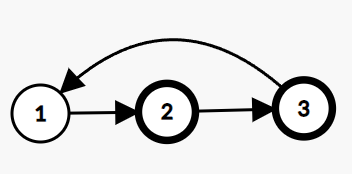
Example:

In the given linked list, there is a cycle, hence we return true.