SDE - 1

You are given a matrix ‘ARR’ with ‘N’ rows and ‘M’ columns. Your task is to find the maximum sum rectangle in the matrix.

Maximum sum rectangle is a rectangle with the maximum value for the sum of integers present within its boundary, considering all the rectangles that can be formed from the elements of that matrix.

For Example

Consider following matrix:

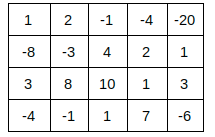
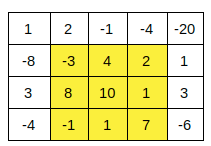
The rectangle (1,1) to (3,3) is the rectangle with the maximum sum, i.e. 29.

You have been given an array 'ARR' of 'N' distinct elements.

Your task is to find the minimum no. of swaps required to sort the array.

For example:

For the given input array [4, 3, 2, 1], the minimum no. of swaps required to sort the array is 2, i.e. swap index 0 with 3 and 1 with 2 to form the sorted array [1, 2, 3, 4].

You are given the schedule of 'N' meetings with their start time 'Start[i]' and end time 'End[i]'.

You have only 1 meeting room. So, you need to return the maximum number of meetings you can organize.

Note:

The start time of one chosen meeting can’t be equal to the end time of the other chosen meeting.

For example:

'N' = 3, Start = [1, 3, 6], End = [4, 8, 7].

You can organize a maximum of 2 meetings. Meeting number 1 from 1 to 4, Meeting number 3 from 6 to 7.

You are given an array/list 'ARR' consisting of N integers, which contains elements only in the range 0 to N - 1. Some of the elements may be repeated in 'ARR'. Your task is to find all such duplicate elements.

Note:

1. All the elements are in the range 0 to N - 1.
2. The elements may not be in sorted order.
3. You can return the duplicate elements in any order.
4. If there are no duplicates present then return an empty array.

Given an integer ‘N’ representing the number of pairs of parentheses, Find all the possible combinations of balanced parentheses with the given number of pairs of parentheses.

Note :

Conditions for valid parentheses:
1. All open brackets must be closed by the closing brackets.

2. Open brackets must be closed in the correct order.

For Example :

()()()() is a valid parentheses.
)()()( is not a valid parentheses.

Given a binary tree, convert this binary tree into its mirror tree.

A binary tree is a tree in which each parent node has at most two children.

Mirror of a Tree: Mirror of a Binary Tree T is another Binary Tree M(T) with left and right children of all non-leaf nodes interchanged.

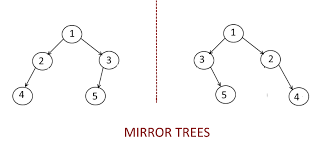
Note:

1. Make in-place changes, that is, modify the nodes given a binary tree to get the required mirror tree.

Give a real-world example of Abstraction and Encapsulation. Also, please differentiate between them. (Learn)

Explain the four pillars of the OOPS. (Learn)

What are static variables and class? (Learn)

Explain Maps in C++. (Learn)

Explain any one of your project? Why you have use react Js in this project.

You are given a string 'S'. Your task is to partition 'S' such that every substring of the partition is a palindrome. You need to return all possible palindrome partitioning of 'S'.

Note: A substring is a contiguous segment of a string.

For Example:

For a given string “BaaB”
3 possible palindrome partitioning of the given string are:
{“B”, “a”, “a”, “B”}
{“B”, “aa”, “B”}
{“BaaB”}
Every substring of all the above partitions of “BaaB” is a palindrome.

You are given a 'Binary Tree'.

Return the bottom view of the binary tree.

Note :

1. A node will be in the bottom-view if it is the bottom-most node at its horizontal distance from the root. 

2. The horizontal distance of the root from itself is 0. The horizontal distance of the right child of the root node is 1 and the horizontal distance of the left child of the root node is -1. 

3. The horizontal distance of node 'n' from root = horizontal distance of its parent from root + 1, if node 'n' is the right child of its parent.

4. The horizontal distance of node 'n' from root = horizontal distance of its parent from the root - 1, if node 'n' is the left child of its parent.

5. If more than one node is at the same horizontal distance and is the bottom-most node for that horizontal distance, including the one which is more towards the right.

Example:

Input: Consider the given Binary Tree:

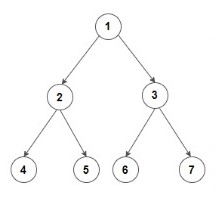
Output: 4 2 6 3 7

Explanation:
Below is the bottom view of the binary tree.

1 is the root node, so its horizontal distance = 0.
Since 2 lies to the left of 0, its horizontal distance = 0-1= -1
3 lies to the right of 0, its horizontal distance = 0+1 = 1
Similarly, horizontal distance of 4 = Horizontal distance of 2 - 1= -1-1=-2
Horizontal distance of 5 = Horizontal distance of 2 + 1=  -1+1 = 0
Horizontal distance of 6 = 1-1 =0
Horizontal distance of 7 = 1+1 = 2

The bottom-most node at a horizontal distance of -2 is 4.
The bottom-most node at a horizontal distance of -1 is 2.
The bottom-most node at a horizontal distance of 0 is 5 and 6. However, 6 is more towards the right, so 6 is included.
The bottom-most node at a horizontal distance of 1 is 3.
The bottom-most node at a horizontal distance of 2 is 7.

Hence, the bottom view would be 4 2 6 3 7

Explain Insertion sort, merge sort, and heap sort. Discuss algorithmic space complexity and auxiliary space complexity. (Learn)

Explain AVL trees. (Learn)

Explain B+ trees. (Learn)

Explain B trees. (Learn)

What are the differences between a B+ and a B tree? (Learn)

What are joins? (Learn)

What is the difference between HTML and React event handling?

Differentiate between process.nextTick() and setImmediate()?