Tata1mg interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Tata1mg
2 rounds | 6 Coding
problems
Interview preparation journey
Preparation
Duration: 5 months
Topics: Data Structures, Pointers, OOPS, System Design, Algorithms, Dynamic Programming
Tip
Tip 1 : Do at least 2-3 Development Projects as it creates a great impression.
Tip 2 : Do it simply don't include complex terms to explain anything/concept.
Tip 3 : Practice as many questions as you can.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : In the projects section, keep a maximum of 3 projects, but ensure that at least one of them is hosted/live that can be shown to the interviewer.
Tip 2 : Do not put false things on resume.
Interview rounds
01
Round
Medium
Online Coding Test
Duration90 minutes
Interview date3 Dec 2021
Coding problem3
There were a total of 3 coding questions to be solved, and the time limit was 90 minutes. I was able to do only two of them completely.
1. Longest Increasing Subsequence
Moderate
0/80
Asked in companies



'N' students are standing in a row. You are given the height of every student standing in the row. Your task is to find the longest strictly increasing subsequence of heights from the row such that the relative order of the students does not change.
A subsequence is a sequence that can be derived from another sequence by deleting zero or more elements without changing the order of the remaining elements.
Problem approach
The simulation of approach will make things clear:
Input : arr[] = {3, 10, 2, 11}
LIS[] = {1, 1, 1, 1} (initially)
Iteration-wise simulation :
arr[2] > arr[1] {LIS[2] = max(LIS [2], LIS[1]+1)=2}
arr[3] < arr[1] {No change}
arr[3] < arr[2] {No change}
arr[4] > arr[1] {LIS[4] = max(LIS [4], LIS[1]+1)=2}
arr[4] > arr[2] {LIS[4] = max(LIS [4], LIS[2]+1)=3}
arr[4] > arr[3] {LIS[4] = max(LIS [4], LIS[3]+1)=3}
We can avoid recomputation of subproblems by using tabulation
2. Capacity To Ship Packages Within D Days
Moderate
15m average time
85% success
0/80
Asked in companies



You are the owner of a Shipment company. You use conveyor belts to ship packages from one port to another. The packages must be shipped within 'd' days.
The weights of the packages are given in an array 'weights'. The packages are loaded on the conveyor belts every day in the same order as they appear in the array. The loaded weights must not exceed the maximum weight capacity of the ship.
Find out the least-weight capacity so that you can ship all the packages within 'd' days.
Problem approach
The given problem can be solved by using the Greedy Technique and Binary Search. The monotonicity of the problem can be observed that if all packages can be successfully shipped within D days with capacity K, then definitely they can be shipped with any capacity larger than K. Follow the steps below to solve the problem:
Initialize a variable, say ans as -1 to store the resultant minimum capacity of the boat required.
Initialize two variables, say s and e with the maximum element in the given array and the total sum of the array respectively which denotes the lower and upper bounds of the search space.
Iterate until the value of s is less than or equals to e, and perform the following steps:
Initialize a variable, say mid as (s + e)/2.
Check if it is possible to ship all the packages within D days when the maximum capacity allowed is mid. If found to be true, then update the value of ans to mid and the value of e to (mid – 1).
Otherwise, update the value of s to (mid + 1).
After completing the above steps, print the value of ans as the result.
3. Maximum Size Rectangle Sub-matrix With All 1's
Hard
10m average time
80% success
0/120
Asked in companies


You are given an 'N' * 'M' sized binary-valued matrix 'MAT, where 'N' is the number of rows and 'M' is the number of columns. You need to return the maximum size (area) of the submatrix which consists of all 1’s i.e. the maximum area of a submatrix in which each cell has only the value ‘1’.
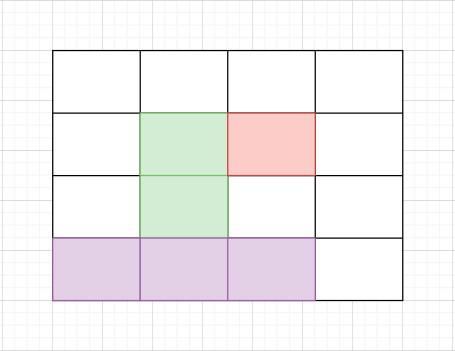
In the above image, areas in green, red, and violet color are all submatrices of the original 4x4 matrix.
Note:
1. Binary valued matrix has only two values in each cell : 0 and 1.
2. A submatrix is a matrix formed by selecting certain rows and columns from a larger matrix.
3. The area of a matrix with 'h' rows and 'w' columns is equal to 'h' * 'w'.
Problem approach
If the height of bars of the histogram is given then the largest area of the histogram can be found. This way in each row, the largest area of bars of the histogram can be found. To get the largest rectangle full of 1’s, update the next row with the previous row and find the largest area under the histogram, i.e. consider each 1’s as filled squares and 0’s with an empty square and consider each row as the base.
Algorithm :-
Run a loop to traverse through the rows.
Now If the current row is not the first row then update the row as follows, if matrix[i][j] is not zero then matrix[i][j] = matrix[i-1][j] + matrix[i][j].
Find the maximum rectangular area under the histogram, consider the ith row as heights of bars of a histogram. This can be calculated as given in this article Largest Rectangular Area in a Histogram
Do the previous two steps for all rows and print the maximum area of all the rows.
02
Round
Medium
Video Call
Duration60 minutes
Interview date7 Dec 2021
Coding problem3
The interviewer asked about the projects I did. After an introductory discussion on projects, he gave me 3 coding questions on their personal live code environment. He also asked me some DSA related theory based questions
1. Trapping Rain Water
Moderate
15m average time
80% success
0/80
Asked in companies



You have been given a long type array/list 'arr’ of size 'n’.
It represents an elevation map wherein 'arr[i]’ denotes the elevation of the 'ith' bar.
Print the total amount of rainwater that can be trapped in these elevations.
Note :
The width of each bar is the same and is equal to 1.
Example:
Input: ‘n’ = 6, ‘arr’ = [3, 0, 0, 2, 0, 4].
Output: 10
Explanation: Refer to the image for better comprehension:

Note :
You don't need to print anything. It has already been taken care of. Just implement the given function.
Problem approach
Approach: In the previous solution, to find the highest bar on the left and right, array traversal is needed, which reduces the efficiency of the solution. To make this efficient, one must pre-compute the highest bar on the left and right of every bar in linear time. Then use these pre-computed values to find the amount of water in every array element.
Algorithm:
Create two arrays left and right of size n. create a variable max_ = INT_MIN.
Run one loop from start to end. In each iteration update max_ as max_ = max(max_, arr[i]) and also assign left[i] = max_
Update max_ = INT_MIN.
Run another loop from end to start. In each iteration update max_ as max_ = max(max_, arr[i]) and also assign right[i] = max_
Traverse the array from start to end.
The amount of water that will be stored in this column is min(a,b) – array[i],(where a = left[i] and b = right[i]) add this value to total amount of water stored
Print the total amount of water stored.
2. The Celebrity Problem
Moderate
30m average time
60% success
0/80
Asked in companies



There are ‘N’ people at a party. Each person has been assigned a unique id between 0 to 'N' - 1(both inclusive). A celebrity is a person who is known to everyone but does not know anyone at the party.
Given a helper function ‘knows(A, B)’, It will returns "true" if the person having id ‘A’ know the person having id ‘B’ in the party, "false" otherwise. Your task is to find out the celebrity at the party. Print the id of the celebrity, if there is no celebrity at the party then print -1.
Note:
1. The helper function ‘knows’ is already implemented for you.
2. ‘knows(A, B)’ returns "false", if A doesn't know B.
3. You should not implement helper function ‘knows’, or speculate about its implementation.
4. You should minimize the number of calls to function ‘knows(A, B)’.
5. There are at least 2 people at the party.
6. At most one celebrity will exist.
Problem approach
Approach:
Model the solution using graphs. Initialize indegree and outdegree of every vertex as 0. If A knows B, draw a directed edge from A to B, increase indegree of B and outdegree of A by 1. Construct all possible edges of the graph for every possible pair [i, j]. There are NC2 pairs. If a celebrity is present in the party, there will be one sink node in the graph with outdegree of zero and indegree of N-1.
Algorithm:
Create two arrays indegree and outdegree, to store the indegree and outdegree
Run a nested loop, the outer loop from 0 to n and inner loop from 0 to n.
For every pair i, j check if i knows j then increase the outdegree of i and indegree of j
For every pair i, j check if j knows i then increase the outdegree of j and indegree of i
Run a loop from 0 to n and find the id where the indegree is n-1 and outdegree is 0
3. Cut Into Segments
Moderate
25m average time
75% success
0/80
Asked in companies



You are given an integer ‘N’ denoting the length of the rod. You need to determine the maximum number of segments you can make of this rod provided that each segment should be of the length 'X', 'Y', or 'Z'.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
4 rounds | 8 problems
Interviewed by Tata1mg
1282 views
1 comments
0 upvotes
SDE - 1
3 rounds | 5 problems
Interviewed by Tata1mg
1323 views
0 comments
0 upvotes
SDE - 1
1 rounds | 3 problems
Interviewed by Tata1mg
1650 views
1 comments
0 upvotes
SDE - 1
4 rounds | 12 problems
Interviewed by Tata1mg
0 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114869 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58031 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35057 views
7 comments
0 upvotes







