SDE - 1

Shrey has just arrived in the city. When he entered the city, he was given two strings. Now, after arriving at his college, his professor gave him an extra string. To check his intelligence, his professor told him to check if the third string given to him has all the characters of the first and second strings in any order. Help Shrey before his professor scolds him. He has to answer “YES” if all characters are present else “NO”.

Example: ‘HELLO’ and ‘SHREY’ are two initial strings, and his professor gave him ’HLOHEELSRY’. So, here all the characters are present, so he has to say “YES”.

Note: The strings contain only uppercase Latin characters.

Given an array/list of integer numbers 'CHOCOLATES' of size 'N', where each value of the array/list represents the number of chocolates in the packet. There are ‘M’ number of students and the task is to distribute the chocolate to their students. Distribute chocolate in such a way that:

1. Each student gets at least one packet of chocolate.

2. The difference between the maximum number of chocolate in a packet and the minimum number of chocolate in a packet given to the students is minimum.

Example :

Given 'N' : 5 (number of packets) and 'M' : 3 (number of students)

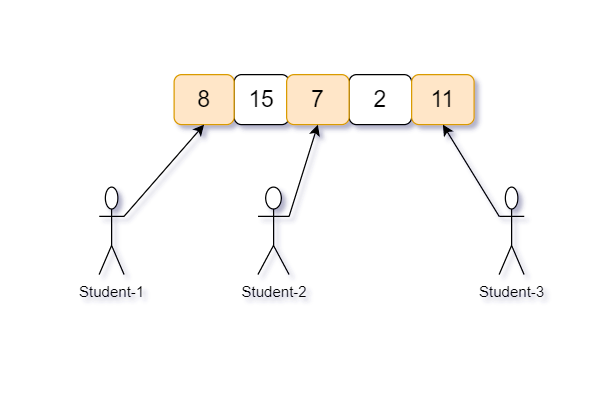
And chocolates in each packet is : {8, 11, 7, 15, 2}

All possible way to distribute 5 packets of chocolates among 3 students are -

( 8,15, 7 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 8, 15, 2 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’ 
( 8, 15, 11 ) difference of maximum-minimum is ‘15 - 8’ = ‘7’
( 8, 7, 2 ) difference of maximum-minimum is ‘8 - 2’ = ‘6’
( 8, 7, 11 ) difference of maximum-minimum is ‘11 - 7’ = ‘4’
( 8, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’
( 15, 7, 2 ) difference of maximum-minimum is ‘15 - 2’ = 13’
( 15, 7, 11 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 15, 2, 11 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’
( 7, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’

Hence there are 10 possible ways to distribute ‘5’ packets of chocolate among the ‘3’ students and difference of combination (8, 7, 11) is ‘maximum - minimum’ = ‘11 - 7’ = ‘4’ is minimum in all of the above.

Given an integer N, print all the prime numbers that lie in the range 2 to N (both inclusive).

Print the prime numbers in different lines.

You have been given a Binary Tree of 'N'

nodes, where the nodes have integer values.

Your task is to return the ln-Order, Pre-Order, and Post-Order traversals of the given binary tree.

For example :

For the given binary tree:

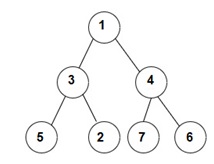
The Inorder traversal will be [5, 3, 2, 1, 7, 4, 6].
The Preorder traversal will be [1, 3, 5, 2, 4, 7, 6].
The Postorder traversal will be [5, 2, 3, 7, 6, 4, 1].

You have been given a binary tree of 'N' nodes. Print the Spiral Order traversal of this binary tree.

For example

For the given binary tree [1, 2, 3, -1, -1, 4, 5, -1, -1, -1, -1]
    1
   / \
  2   3
     / \
    4   5

Output: 1 3 2 4 5

You are given a 2-dimensional array/list having N rows and M columns, which is filled with ones(1) and zeroes(0). 1 signifies land, and 0 signifies water.

A cell is said to be connected to another cell, if one cell lies immediately next to the other cell, in any of the eight directions (two vertical, two horizontal, and four diagonals).

A group of connected cells having value 1 is called an island. Your task is to find the number of such islands present in the matrix.

You have been given a Snake and Ladder Board with 'N' rows and 'N' columns with the numbers written from 1 to (N*N) starting from the bottom left of the board, and alternating direction each row.

For example

For a (6 x 6) board, the numbers are written as follows:

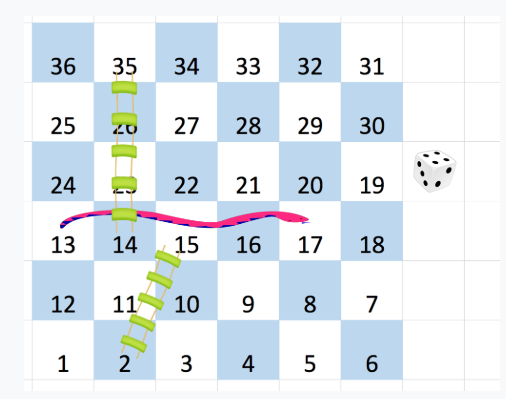
You start from square 1 of the board (which is always in the last row and first column). On each square say 'X', you can throw a dice which can have six outcomes and you have total control over the outcome of dice throw and you want to find out the minimum number of throws required to reach the last cell.
Some of the squares contain Snakes and Ladders, and these are possibilities of a throw at square 'X':
You choose a destination square 'S' with number 'X+1', 'X+2', 'X+3', 'X+4', 'X+5', or 'X+6', provided this number is <= N*N.
If 'S' has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.
A board square on row 'i' and column 'j' has a "Snake or Ladder" if board[i][j] != -1. The destination of that snake or ladder is board[i][j].

Note :

You can only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving - you have to ignore the snake or ladder present on that square.

For example, if the board is:
-1 1 -1
-1 -1 9
-1 4 -1
Let's say on the first move your destination square is 2  [at row 2, column 1], then you finish your first move at 4 [at row 1, column 2] because you do not continue moving to 9 [at row 0, column 0] by taking the ladder from 4.

A square can also have a Snake or Ladder which will end at the same cell.
For example, if the board is:
-1 3 -1
-1 5 -1
-1 -1 9
Here we can see Snake/Ladder on square 5 [at row 1, column 1] will end on the same square 5.

It was mainly around my projects, past internships & experience.