Problem
Submissions
Hints & solutions
Discuss
All Paths From Source Lead To Destination
Moderate
0/80
Average time to solve is 30m
8 upvotes
Asked in companies



Problem statement
There is a directed graph consisting of ‘N’ nodes numbered from 0 to ‘N’-1. You are given a list ‘EDGES’ of size ‘M’, consisting of all the edges of this directed graph, and two nodes ‘SRC’ and ‘DEST’ of this graph. Determine whether or not all paths starting from node ‘SRC’ eventually end at node ‘DEST’, that is -:
1. At least one path exists from node ‘SRC’ to node ‘DEST’.
2. If there exists a path from the node ‘SRC’ to a node with no outgoing edges, then that node must be ‘DEST’.
3. There should be a finite number of paths from ‘SRC’ to ‘DEST’.
You should return True if all paths starting from node ‘SRC’ eventually end at node ‘DEST’, Otherwise, return False. See the example for more clarity.
Note :
1. The given graph may have self-loops and parallel edges.
Consider ‘N’ = 4, ‘EDGES’ = [[0, 1], [0, 3], [1, 2], [3, 2]], ‘SRC’ = 0 and ‘DEST’ = 2. The given directed graph is shown below.
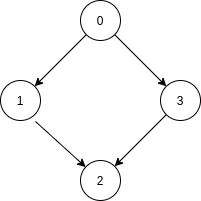
Here, all the paths that start from node 0 are -:
1. 0->1->2
2. 0->3->2
Both of these paths eventually end at node ‘2’ i.e node ‘DEST’. Thus we should return True.
Detailed explanation ( Input/output format, Notes, Images )
Input format :
The first line of input contains an integer ‘T’ denoting the number of test cases. then ‘T’ test cases follow.
The first line of each test case consists of four single space-separated integers ‘N’, ‘M’, ‘SRC’, ‘DEST’, described in the problem statement.
Then next ‘M’ lines follow in each test case. The ith line consists of two space-separated integers ‘EDGES[i][0]’ and ‘EDGES[i][1]’ representing that there is a directed edge from node ‘EDGES[i][0]’ to ‘EDGES[i][1]’.
For each test case, print a string “True” if all paths starting from node ‘SRC’ eventually end at node ‘DEST’, Otherwise, print “False”.
Print output of each test case in a separate line.
Note :
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints :
1 <= T <= 50
2 <= N <= 10^4
0 <= M <= 10^4
0 <= SRC < N
0 <= DEST < N
SRC != DEST
0 <= EDGES[i][j] < N.
Where ‘T’ is the total number of test cases, ‘N’, ‘M’, ‘SRC’, and ‘DEST’ are as described in the problem statement. ‘EDGES[i][j]’ is an integer in list ‘EDGES’.
Time limit: 1 sec
Sample Input 1 :
3
2 2 0 1
0 0
0 1
3 2 0 1
0 1
1 2
4 4 0 2
0 1
0 3
1 2
3 2
Sample Output 1:
False
False
True
Explanation of Sample Input 1:
For test case 1, there is a self-loop at node 0, thus the number of paths starting from node 0 cannot be finite. Thus we should return false. (See condition 3 in the problem statement).
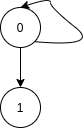
For test case 2, the only path that starts from 0 is 0->1->2, This path ends at 2, instead of 1.
For test case 3, see the problem statement for an explanation.
Sample Input 2:
2
5 3 3 2
1 2
3 2
2 1
5 3 3 2
1 2
3 2
3 1
Sample Output 2:
False
True
Hint
Hint 1
Can we use Depth First Search to solve this problem?
Approaches (1)
Approach 1
Depth First Search
All the paths starting from node ‘SRC’ eventually end at node ‘DEST’ if -:
- Node ‘DEST’ is reachable from ‘SRC’.
- There is no outgoing edge from node ‘DEST’.
- No cycle is reachable from ‘SRC’.
We can check these conditions using the Depth First Search algorithm as follows -:
Algorithm
- Create a list of lists ‘ADJ’ of size ‘N’.
- Create an adjacency list of the given directed graph. This can be done by running a loop where ‘i’ ranges from 0 to ‘M’-1 and for each ‘i’ push EDGES[i][1] in list ADJ[EDGES[i][0]].
- If ADJ[DEST] is not empty, return false as there should be no outgoing edge from node ‘DEST’.
- Created a boolean array/list VISITED of size ‘N’, initially fill it with false.
- Created a boolean array/list RECSTK of size ‘N’ to track recursion stack while DFS, initially fill it with false.
- Run a depth-first search algorithm by calling a recursive function, named DFS(‘CUR’, ‘DEST’, ‘VISITED’, ‘RECSTK, ‘ADJ’ ). It will return True if all the paths starting from node ‘CUR’ eventually end at node ‘DEST’ In each recursive call of this function, we will do the following steps.
- If ‘CUR’ = ‘DEST’, then return True.
- If ‘ADJ[CUR]’ is empty, then return False, because the path ends at a node other than ‘DEST’.
- Do VISITED[‘CUR’]:= True, and RECSTK[‘CUR’]:= True.
- Iterate over ADJ[‘CUR’] and for each node ‘V’ in it do the following -:
- If RECSTK[‘V’] is True then return False, because the cycle is detected.
- If VISITED[‘V’] is False, then recursively call DFS(‘V’, ‘DEST’, ‘VISITED’ ‘ADJ’ ). Return False, if this recursive call to DFS returns False.
- Do RECSTK[‘CUR’]:= False, and return True.
- Return DFS(‘SRC’, ‘DEST’, ‘VISITED’, ‘RECSTK, ‘ADJ’ ).
Time Complexity
O(N + M), where ‘N’ is the number of nodes and ‘M’ is the number of edges.
DFS takes O(N + M) times and creating an adjacency list will also take O(N + M) times, Thus overall time complexity will be O(N + M).
Space Complexity
O(N + M), where ‘N’ is the number of nodes and ‘M’ is the number of edges.
Extra space used by adjacency list ‘ADJ’ is of size O(N + M), and recursion stack, list ‘VISITED’ and ‘RECSTK’ use O(N) space, Thus overall space complexity will be O(N + M).
Code Solution
(100% EXP penalty)
All Paths From Source Lead To Destination
C++ (g++ 5.4)
Console
