Problem
Submissions
Hints & solutions
Discuss
All Root to Leaf Paths In Binary Tree.
Moderate
0/80
Average time to solve is 25m
Problem statement
You are given an arbitrary binary tree consisting of 'N' nodes numbered from 1 to 'N'. Your task is to print all the root to leaf paths of the binary tree.
A leaf of a binary tree is the node which does not have a left child and a right child.
Given a binary tree :
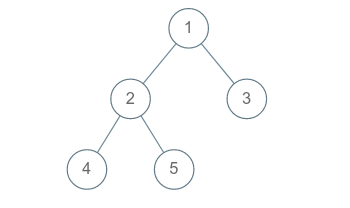
All the root to leaf paths are :
1 2 4
1 2 5
1 3
Note :
1. Two nodes may have the same value associated with it.
2. The root node will be fixed and will be provided in the function.
3. Note that the nodes in a path will appear in a fixed order. For example, 1 2 3 is not the same as 2 1 3.
4. Each path should be returned as a string consisting of nodes in order and separated by a space.
5. The path length may be as small as ‘1’.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line contains an integer 'N', which denotes the number of nodes in the tree.
The second line will contain the values of the nodes of the tree in the level order form ( -1 for 'NULL' node) Refer to the example for further clarification.
Consider the binary tree
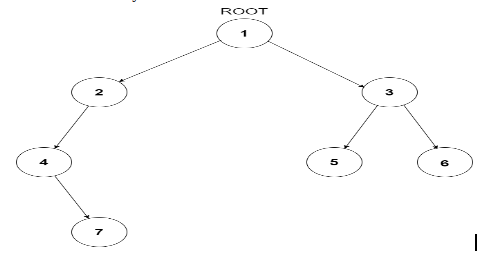
The input of the tree depicted in the image above will be like :
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Print all the root to leaf path nodes.
You do not need to print anything, it has already been taken care of. Just implement the given function.
Sample Input 1 :
5
1 2 3 4 5 -1 -1 -1 -1 -1 -1
Sample Output 1 :
1 2 4
1 2 5
1 3
Explanation for Sample Input 1:

All the root to leaf paths are :
1 2 4
1 2 5
1 3
Sample Input 2 :
7
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Sample Output 2 :
1 3 5
1 3 6
1 2 4 7
Constraints :
1 <= N <= 3*10^3
Time Limit : 1 sec
Hint
Hint 1
Hint 2
Try doing Depth-First Search.
Approaches (2)
Approach 1
Approach 2
Depth-First Search
- We can use a depth-first approach to solve this problem since the tree is a recursive data structure.
- Let us create a recursive function ‘DFS’() which takes the root of the tree and the current string curr for maintaining the current path as the parameter.
- ‘DFS’() traverses the binary tree and stores the root to leaf paths. When we hit a leaf node, we can simply store the current string in some data structure as this string represents a valid root to leaf path
- Now we can return use the ‘RESULT’ list containing all the root to leaf paths in the form of strings.
Time Complexity
O(N), where ‘N’ is the number of nodes in the tree.
We traverse all the nodes of the binary tree to find the paths. Therefore, the overall time complexity will be O(N).
Space Complexity
O(N), where ‘N’ is the maximum height of a binary tree.
Recursive stack for storing paths can contain at most nodes of height of a binary tree which in worst can be equal to ‘N’ (skewed tree). Therefore, the overall space complexity will be O(N).
Code Solution
(100% EXP penalty)
All Root to Leaf Paths In Binary Tree.
Javascript (node v10.20.0)
Console



