Problem
Submissions
Hints & solutions
Discuss
Area Under Curve
Moderate
0/80
Average time to solve is 30m
Problem statement
Given a curve whose edges are parallel to either X-axis or Y-axis, you need to find the area under this curve along the X-axis. The curve will be given in the form of a linked list containing N nodes, where each node represents the coordinates of the curve.
The area under the curve along the X-axis is defined as the total area covered by the curve and the line Y = 0. See the sample explanation figure below for further clarification.
Note1. The coordinates will be given in non-descending order of X coordinate from start to end of the linked list.
2. All the coordinates will be pairwise distinct i.e there are no two coordinates (X1, Y1) and (X2, Y2) such that X1 = X2 and Y1 = Y2 and there will be an edge between every two consecutive coordinates.
3. The first coordinate and the last coordinate in the input can be assumed as the starting point and the ending point of the curve respectively and there will not be an edge between these two coordinates.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains a single integer T denoting the number of test cases.
The first and the only line of each test case will contain 2 * N +1 linked list elements (separated by space and terminated by -1), where 'N' is the total number of coordinates.
Each node consists of two parts (X coordinate and Y coordinate).
For each test case, print a single integer denoting the total area under the given curve.
You do not need to print anything, it has already been taken care of. Just implement the given function and return the answer.
Constraints:
1 <= T <= 10
1 <= N <= 10^4
-10^4 <= X, Y <= 10^4
Time Limit: 1 sec
Sample Input 1:
2
1 10 5 10 7 10 7 5 20 5 40 5 40 7 42 7 -1
0 0 -1
Sample Output 1:
239
0
Explanation For Sample Input 1:
For the first test:
The curve can be represented on a X - Y plane as follows:
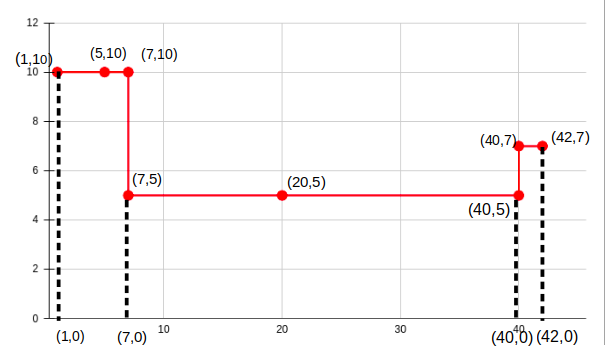
Clearly we can divide the area under this curve into 3 rectangles of dimensions:
6 X 10 , 33 X 5 and 2 X 7. Thus the total area is 6 * 10 + 33 * 5 + 2* 7 = 239.
For the second test:
As there is only one point in the curve and which is the origin the area here will be zero.
Sample Input 2:
2
2 4 2 4 5 4 -1
4 5 2 3 -1
Sample Output 2:
12
0
Hint
Hint 1
Can you try forming a shape with two coordinates?
Approaches (1)
Approach 1
Two Coordinates
- As given in the problem statement, the edges of the curve will always be parallel to either of the two axes, so we can assume that for every two consecutive coordinates either the X-coordinate or the y-coordinate will be the same for them.
- Thus we can always imagine a rectangle between every two consecutive coordinates of the curve and the corresponding coordinates on the X-axis.
- If the x-coordinate of the two consecutive points are the same, then the area of the rectangle formed will be 0, otherwise, the area will be (X2 - X1) * Y, where Y is the Y-coordinate of both the points and X1 and X2 are X-coordinates of first and the second point respectively.
Time Complexity
O(N), where N is the number of coordinates in the input.
As we are processing each coordinate only once, thus the total complexity will be proportional to the total number of coordinates. hence the time complexity is O(N).
Space Complexity
O(1)
As constant extra space is used.
Code Solution
(100% EXP penalty)
Area Under Curve
Javascript (node v10.20.0)
Console



