Binary Tree from Parent Array

Easy
0/40
Average time to solve is 15m
16 upvotes
Asked in companies
SAP LabsTraveloka

Problem statement

Given an array parent which represents a binary tree such that parent-child relationship is defined by ('PARENT'[i], 'i') which means that parent of i is 'PARENT'[i]. The value of the root node will be i if -1 is present at 'PARENT'[i].

For example:

For the parent array {1, -1, 1}, the tree will be:-

1

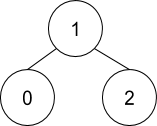
As, parent of 0 is 'PARENT'[0] i.e. 1.
1 is the root as 'PARENT'[1] = -1.
Parent of 2 is 'PARENT'[2] i.e. 1.

Similarly for the parent array { 1, 2, -1}, the tree will be:-

2

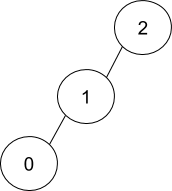
Your task is to create the Binary tree from the given parent array.

Note:

From the parent array, multiple binary trees may be possible. You have to create a binary tree in such a way that these conditions satisfy:-

If the node has a left child as well as a right child, make sure the left child is smaller than the right child. 

If the node has only one child, make sure it has an only left child. 

For {1, -1, 1}, the accepted tree will be:-

3

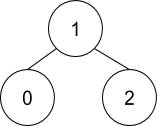
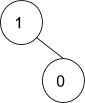
And for {1, -1}, the accepted tree will be,

4

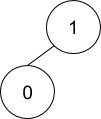
Instead of

5

Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer 'T' denoting the number of queries or test cases. 

The first line of every test case contains an integer 'N' denoting the size of the parent array. 

The second line of every test case contains 'N' single space-separated integers, representing the elements of the parent array.
Output format: 
For each test case, print the level order of the Binary tree in a separate line. 

For example, the level order output for the tree depicted in the below image would be :

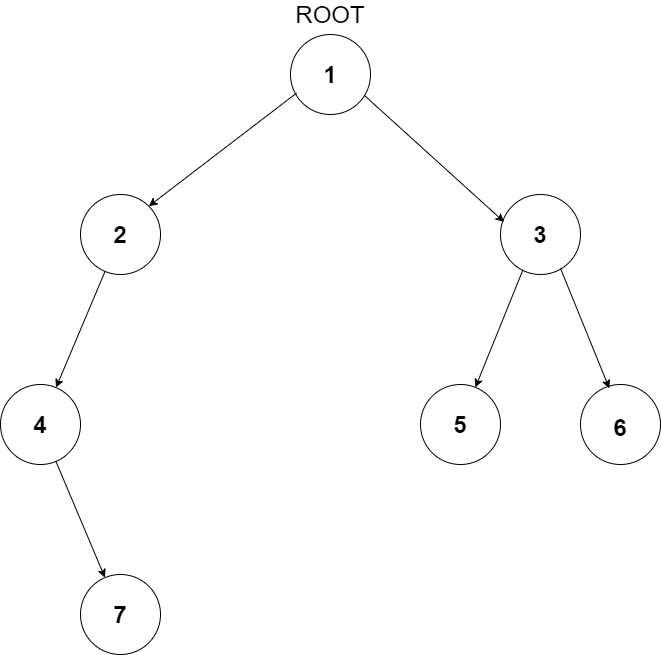
alt text

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :

Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Note : 
The above format was just to provide clarity on how the output is formed for a given tree. 

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= 'T' <= 100
1 <= 'N' <= 3000

Where 'T' is the number of test cases and 'N' denotes the number of nodes in the tree.

Time limit: 1 sec.
Sample input 1:
2
2
1 -1 
6
-1 0 1 2 2 3
Sample output 1:
1 0 -1 -1 -1 
0 1 -1 2 -1 3 4 5 -1 -1 -1 -1 -1
Explanation for Sample Input 1:
For test case 2: The resulting tree will be:-

6

Sample input 2:
2
4
2 3 3 -1 
7  
1 5 5 2 2 -1 3
Sample output 2:
3 1 2 -1 -1 0 -1 -1 -1
5 1 2 0 -1 3 4 -1 -1 6 -1 -1 -1 -1 -1
Hint

We can observe that we can get the root node only by searching for -1 in the array. According to the properties of a binary tree, it will have at max 2 children, thus you can search for the two children and assign children to the parent nodes. Repeatedly following the above point will end up fetching you the final binary tree. 

Approaches (2)
Brute force

The idea here is to repeatedly find out the children of a particular node, attach them with their 'PARENT' node and work on the child nodes separately.

  • This can be achieved by:-
    • Find out the 'ROOT' node by searching for ‘-1’ in the given 'PARENT' array.
      Pass this 'ROOT' node as well as the 'PARENT' array into a helper function.
      The helper function returns us the final 'ROOT' of the binary tree by doing the following things:-
    • If the 'ROOT' is 'NULL', i.e. we are given the 'PARENT' array of a 'NULL' tree, returns 'NULL'.
      Otherwise, traverses the 'PARENT' array and finds out the children of the current 'ROOT'. Let us store 'LEFT' child in 'FIRST' and 'RIGHT' child in Second.
      Assigns 'FIRST' to the 'LEFT' child of 'ROOT' and recursively calls for the creation of subtree which has 'FIRST' as its 'ROOT'.
      Assigns Second to the 'RIGHT' child of 'ROOT' and recursively calls for the creation of subtree which has Second as its 'ROOT'.
      Return the 'ROOT' fetched from the helper function.
  • Algorithm:
  • Node 'CREATETREE'('PARENT'[]):
    • Traverse the whole array and find out the 'ROOT' node i.e. store 'INDEX' when 'PARENT'['INDEX'] = -1.
      Create a new 'ROOT' node with value 'INDEX'.
      Call 'CREATETREE'Helper('ROOT', 'PARENT') and store it in a Node say ans.
      Return ans.
    • Node* 'CREATETREEHELPER'( 'ROOT', List 'PARENT'[] ):
  • If the 'ROOT' is 'NULL', return 'NULL'.
     
  • Create Tree nodes that say 'FIRST' and second.
    Search for 'LEFT' and 'RIGHT' child i.e if: 'PARENT'['INDEX'] == 'ROOT'->data, 
     
  • For 'FIRST' time, 'FIRST' = Node('INDEX') 
     
  • For second time, second = Node('INDEX'). 
     
  • 'ROOT'->'LEFT' = 'CREATETREEHELPER'('FIRST', 'PARENT')
     
  • This creates the 'LEFT' subtree recursively.
     
  • 'ROOT'->'RIGHT' = 'CREATETREEHELPER'(second, 'PARENT')
     
  • This creates the 'RIGHT' subtree recursively.
     
  • Return 'ROOT'.
Time Complexity

O(N ^ 2), where ‘N’ is the size of the parent array.

 

In the worst case, the tree we are creating has N nodes and we are traversing at each node recursively, additionally, for every node we are traversing the parent array as well. This makes it N * N.

Space Complexity

O(H), where H is the height of the tree we are creating.

 

Extra space is used by recursion stack which goes up to the height of the resulting tree, which, in the worst case, can go till N i.e. size of the parent array.

Code Solution
(100% EXP penalty)
Binary Tree from Parent Array
Full screen
Console