Bipartite Graph

Moderate
0/80
4 upvotes
Asked in companies
ArcesiumDunzoCIS - Cyber Infrastructure

Problem statement

Given an undirected graph of ‘V’ vertices (labeled 0,1,..., V-1) and ‘E’ edges . Your task is to check whether the graph is bipartite or not.

A bipartite graph is a graph whose vertices can be divided into two sets such that each edge of the graph connects one vertex from the first set and another vertex from the second set.
We can also define a bipartite graph as a graph which can be colored using two colors such that no two adjacent vertices have the same color. 

For example: 
Input: 
4 4
0 1
0 2
1 3
2 3

An undirected graph to the above input is shown below:


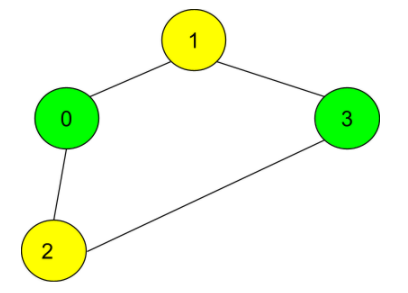
In the given input, the number of vertices is 4, and the number of edges is 4.
In the input, following the number of vertices and edges, a list of pairs of numbers is given where each pair (u, v) denotes an edge between vertex u and v.
As per the input, there is an edge between vertex 0 and vertex 1.
The vertices 0 and 2 have an edge between them.

The vertices 1 and 3 have an edge between them.
The vertices 2 and 3 have an edge between them.

As the graph can be colored using two colors, and no adjacent vertices share the same color, the graph is bipartite.
Detailed explanation ( Input/output format, Notes, Images )

Input format:

The first line of input contains an integer ‘T’ denoting the number of test cases.
The first line of each test case contains two integers ‘V’ and ‘E’ denoting the number of vertices in the undirected graph and the number of edges in the undirected graph, respectively. 
The next E lines contain two space-separated integers ‘u’, ‘v’, denoting two vertices connected by an edge.

Output format:

For each test case, return “True” (without quotes) if the given graph is bipartite else return “False”. 
The output of each test case is printed in a separate line.

Note:

1.  There are no parallel edges i.e no two vertices are directly connected by more than 1 edge.
2.  The graph is necessarily undirected. 
3.  You are not required to print the output explicitly, it has already been taken care of. Just implement the function that checks whether the given graph is bipartite or not.
Constraints : 
1 <= T <= 10
2 <= V <= 200
1 <= E <= V * (V - 1)/2
where ‘T’ is the number of test cases,  ‘V’ is the number of vertices, ‘E’ is the number of edges.

Sample Input 1:

1
4 4 
0 1
0 2 
2 3 
1 3

Sample Output 1:

True

Explanation of Sample Input 1:

The graph formed by the given input is shown in the above example. We can clearly see that the graph is colored using two colors only and no adjacent vertices have the same color. It means, we can divide the vertices of the graph in two sets such that each edge of the graph connects one vertex from the first set and another vertex from the second set.
First Set: { 0, 2 } 
Second Set: { 1, 3 } 
Hence, the given graph is bipartite and the answer is ‘True’.

Sample Input 2:

1
4 5
0 1
0 2 
1 2
1 3 
2 3

Sample Output 2:

False

Explanation of sample output 2:

The graph formed from the given input is shown below: 


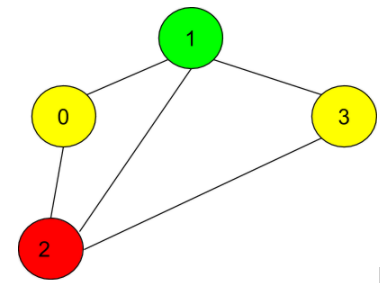
We can't color the vertex 2 by green as it is adjacent to the already green colored vertex 1. Thus, we can’t color the graph using only two colors. It means the graph is not bipartite.
Hint

Use the fact that a bipartite graph can be colored using 2 colors such that no two adjacent vertices have the same color. Can we use DFS to traverse the graph?  

Approaches (3)
DFS

The idea is very simple. To separate the vertices of the graph in two sets such that no two vertices of a set are connected, we will try to color the vertices of the graph using two colors only. 

If any of the adjacent vertices are of the same color, the graph is not bipartite. Else, it is bipartite. 

Note that, if there are more than 1 connected components in the graph, the graph will be bipartite if and only if all the connected components are bipartite. 
 

Algorithm: 

  • We have the edges of the graph and we need to form an adjacency list from this given information. For this, make an adjacency list that will be storing the two nodes between which an edge exists.
  • Create an integer array color of size ‘V’ to keep track of the color assigned the vertices. It can only contain 2 values, 0 or 1. 0 denotes ‘Green’ and 1 denotes ‘Yellow’ color.
  • Create a boolean array of size ‘V’ to keep track of the already visited vertices.
  • To include all the connected components of the graph, loop from 0 to V - 1:
    • If the current vertex is not visited:
      • Assign green color ( 0 )  to the current vertex.
      • Mark the current vertex as visited and traverse its neighbors using the adjacency list and assign yellow color to them.
      • Traverse the neighbor’s neighbor using depth first search and assign them a green color.
      • Repeat this process until all the vertices are assigned a color.
  • During this process, if a neighbor vertex is already visited and has the same color as the current vertex, terminate the process and return ‘False’ as the graph is not bipartite.
  • If we have successfully colored the graph using 2 colors, return ‘True’ as the graph is bipartite.
Time Complexity

O(V + E) where V is the number of vertices in the graph, and E is the number of edges in the graph. 

We are creating an adjacency list which requires O(V + E) time. We are using depth first search for traversing the graph using adjacency list. Scanning for all adjacent vertices takes O(E) time, since the sum of lengths of adjacency lists of all vertices is E. Thus, the total time complexity is O(V + E) + O(V + E) = O(V + E). 

Space Complexity

O(V ^ 2), where V is the number of vertices in the graph. 

We are using an adjacency list. In the worst case, the graph can be proper and the number of edges will be (V * (V - 1) / 2). Thus, the size of the adjacency list will be O(V ^ 2). Space required by the visited array, and the color array is O(V). Also, if the entire graph is traversed in a single recursive call, O(V) recursion stack space is used. Thus, the final space complexity is O(V ^ 2) + O(V) + O(V) = O(V ^ 2).

Code Solution
(100% EXP penalty)
Bipartite Graph
Full screen
Console