Build Binary Expression Tree From Infix Expression

Moderate
0/80
Average time to solve is 15m
2 upvotes
Asked in companies
FacebookMathworks

Problem statement

You are given a string ‘S’, an infix expression that has operands, operators and parentheses ‘(‘ and ‘)’.

You need to return the binary expression tree, whose inorder traversal is the same as ‘S’.

Note:

Infix expression: The expression of the form ‘a operator b’. When an operator is in-between every pair of operands.
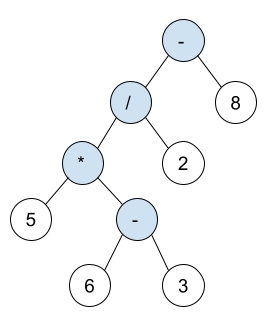
The expression tree is a binary tree in which each internal node corresponds to the operator and each leaf node corresponds to the operand so for example expression tree for 5 * ( 6 - 3 ) / 2 - 8 would be:

Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line of input contains an integer 'T' representing the number of test cases.

The first line of each test case contains a string S representing infix expression.
Output Format : 
For each test case, return the binary expression tree, whose inorder traversal is the same as 'S'. 

Return -1 instead of NULL.

The output for each test case is printed in a separate line.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 5
1 <= N <= 5000
Operands are only numbers between 0 and 9 (included).
It is guaranteed that ‘S’ is a valid infix expression.

Time limit: 1 sec

Sample Input 1:

2
5*(9-4)/7+6
5*7-8/6

Sample Output 1:

[+, /, 6, *, 7, -1, -1, 5, -, -1, -1, -1, -1, 9, 4, -1, -1, -1, -1]
[-, *, /, 5, 7, 8, 6, -1, -1, -1, -1, -1, -1, -1, -1]

Explanation of Sample Output 1:

Test Case 1: The expression tree for the given infix expression will be:


Test Case 2:  The expression tree for the given infix expression will be:

Sample Input 2:

2
7*6/4-2+4
7+(5/9)-6

Sample Output 2:

[+, -, 4, /, 2, -1, -1, *, 4, -1, -1, 7, 6, -1, -1, -1, -1, -1, -1]
[-, +, 6, 7, /, -1, -1, -1, -1, 5, 9, -1, -1, -1, -1]
Hint

Try to use stacks to store the nodes.

Approaches (1)
Implementation

The idea is that we will use two stacks, one for operators and the other for nodes but before all this, we need to first set the priority of each operator. We can use a map to set priority.

After setting the priority we will iterate through all characters of the given string ‘STR’ and we will have 4 cases.

 

  • Case 1: When we encounter an open parenthesis ‘(‘. We just push this character in the operators stack and move on.
  • Case 2: When a digit is encountered then we create a new node and push that in the nodes stack.
  • Case 3: When a close parenthesis is encountered ‘)’ then we will start popping the elements from operators stack till we get an open parenthesis and on each pop, we will make a new node such that the right and left child of the node are top 2 nodes from node stack and push the new node back in the stack.
  • Case 4: When an operator(*, +, -, / ) is encountered. We will again form a new node as we did in the previous case till either operator is empty or the priority of the top element of operators is less than the priority of the current operator.

 

After this if stack size is still greater than 1 then we will make new nodes using operator and node stack till get size = 1 in the node stack.

 

Algorithm:

             map<char,int> priority;

             Set priority of ‘(‘ = 1, ‘-’ = 2, ‘+’ = 2,  ’*’ =3 , ‘/’ = 3     

             stack<char> operators;

             stack<binarytreenode> tree

             foreach(char c of  s){

                 Check for all above cases one by one.

             }

             while(node.size > 1)

             {

                 makeNode(operator, tree).

             }

            return tree.top().

Time Complexity

O(N), where ‘N’ is the length of the given string.

 

We are checking each character of the string one by one.

Space Complexity

O(N), where ‘N’ is the length of the given string.

 

In the worst case, due to parenthesis stack can contain all the operators. 

Code Solution
(100% EXP penalty)
Build Binary Expression Tree From Infix Expression
Full screen
Console