Buildings Projection

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
19 upvotes
Asked in companies
Google incalibabaBritish Telecommunications

Problem statement

Ninja Land can be represented as a N * N grid in the XY plane. Each cell of this grid can have a building of some height.

You are given a matrix ‘GRID[][]’ of size ‘N’ * ‘N’, where ‘GRID[i][j]’ gives the height of the building at cell (i, j) in XY plane. Note, building at any cell (i, j) is represented as a cuboid that is an axis aligned with the axis ‘X’, ‘Y’, ‘Z’ and has the dimension 1 * 1 * GRID[i][j] along X, Y, Z-axis respectively.

Ninja views the projection of these buildings onto the XY, YZ, and ZX planes. A projection is like a shadow, that maps a 3-dimensional figure to a 2-dimensional plane. We are viewing the "shadow" when looking from the top, the side, and the front, in XY, YZ, ZX plane respectively.

Your task is to find and return the total area of all three projections. See the example for more clarity.

Note: 
 ‘GRID[i][j]’ = 0, if there is no building at cell (i, j).
Example: 
Consider the following 2*2 ‘GRID[][]’:
                [1, 2]
                [3, 4]

Its projection in XY, YZ, XZ plane is shown below -:

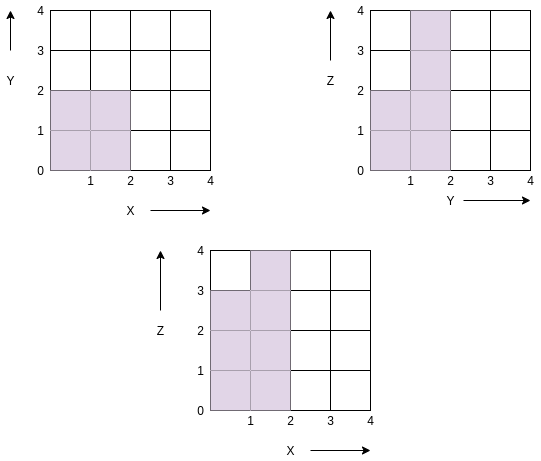
alt text

Area covered in XY plane is 4, Area covered in YZ plane is 6, Area covered in ZX plane is 7, Thus the total area is 4 + 6 + 7 = 17.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains a single integer ‘T’ representing the number of test cases. 

The first line of each test case will contain a single integer ‘N’, representing the dimensions of ‘GRID’ 

The next ‘N’ line of each test case will follow, each contains ‘N’ space-separated integers. These ‘N’ lines together represent the matrix ‘GRID[][]’.
Output Format: 
For each test case, print a single integer that represents the total area of projections in the XY, YZ, and ZX plane.

Output for every test case will be printed in a separate line.
Note: 
You don’t need to print anything; it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 50
2 <= N <= 1000
0 <= GRID[i][j] <= 100

Where ‘GRID[i][j]’ is the height of the building at cell (i, j).

Time limit: 1 sec
Sample Input 1:
2
1
1
2
1 2
3 4
Sample Output 1:
3
17
Explanation of sample input 1:
In the first test case,  there is a 1*1 grid, and its only cell i.e cell (0, 0) has a building of height 1. Thus its projection in all three planes also takes area 1.

For the second test case, see the problem statement for an explanation.
Sample Input 2:
2
3
0 0 0
0 0 0
0 0 0
3
1 1 1
1 0 1
1 1 1
Sample Output 2:
0
14
Hint

Think about the dimension of shadow from the top, side, front independently.

Approaches (1)
Maths

In the XY plane, the shadow made by each building will be 1 square.

 

In the YZ plane, the shadow made will be the largest value for each row in the grid.

 

In the ZX plane, the shadow made will be the largest value for each column in the grid.

 

The steps are as follows:

 

  1. Initialize an integer variable ‘RESULT’:= 0.
  2. Run a loop where ‘i’ ranges from 0 to ‘N’-1 and for each ‘i’ do the following -:
    1. Initialize two Integer variables ‘ROWMAX‘ := 0, ‘COLMAX’: = 0.
    2. Run a loop where ‘j’ ranges from 0 to ‘N’-1 and for each ‘j’ do the following -:
      1. If ‘GRID[i][j]’ > 0 then increment ‘RESULT’ by 1.
      2. Do ‘ROWMAX’ = max(‘ROWMAX’, ‘GRID[i][j]’).
      3. Do ‘COLMAX’ = max(‘COLMAX’, ‘GRID[j][i]’).
    3. Do ‘RESULT’ = ‘RESULT’ + ‘ROWMAX’ + ‘COLMAX’ .
  3. Return ‘RESULT’.
Time Complexity

O(N^2), where 'N' is the dimension of ‘GRID’.

 

We are running two nested loops each of them runs for ‘N’ times, so the overall complexity will be O(N^2). 

Space Complexity

O(1).

 

We are using constant extra space here.

Code Solution
(100% EXP penalty)
Buildings Projection
Full screen
Console