Check for Duplicate Subtree

Hard
0/120
Average time to solve is 15m
profile
Contributed by
7 upvotes
Asked in companies
Flipkart limitedGoogle inc

Problem statement

Given an arbitrary binary tree consisting of N nodes, each node is associated with a character value. Your task is to check whether there exist a pair of nodes such that their subtrees are equal.

Note : 
A subtree of a node X is all the nodes that are below X and X itself.

A binary tree is a tree consisting of at most two children.

Two subtrees are said to be equal if they both have the same structure and the corresponding nodes in both the subtrees are associated with the same character value.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line of each input has a single integer T, denoting the number of test cases.

The first line of each test case contains a single integer N, denoting the number of nodes in a tree.

The second line contains the keys of the nodes of the tree in the level order form ( # for NULL node) Refer to the example for further clarification.
Example: 
Consider the binary tree

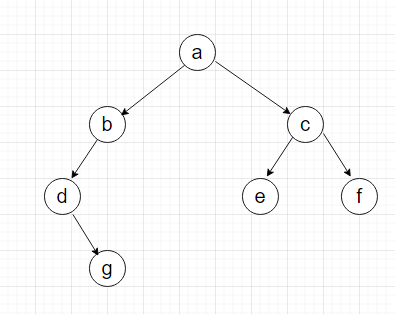
altImage

The input of the tree depicted in the image above will be like: 
a
b c
d # e f
# g # # # #
# #

Explanation :
Level 1 :
The root node of the tree is a

Level 2 :
The left child of a = b
Right child of a = c

Level 3 :
Left child of b= d
Right child of b = null (#)
Left child of c = e
Right child of c = f

Level 4 :
Left child of d = null (#)
Right child of d = g
Left child of e = null (#)
Right child of e = null (#)
Left child of f = null (#)
Right child of f = null (#)

Level 5 :
Left child of g = null (#)
Right child of g = null (#)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (#).
Output format : 
For each test case print on a new line “True”, if there are two similar subtrees with size greater than or equal to 2, otherwise print “False”.
Note : 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 100
1 <= N <= 500
a <= node value <= z

Time Limit: 1 sec.
Sample Input 1 :
1
6
a b a c # b # # # c # # #
Sample Output 1 :
True
Explanation For Sample Input 1:
The given test case represents the following tree.

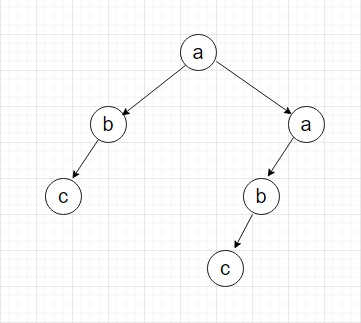
altImage

Here the subtree of 2 and 5 are the same that is 
   b
 /
c
Sample Input 2 :
1
6
a a # a # a # a # a # # #
Sample Output 2 :
False
Hint

Considering all possible pairs 

Approaches (2)
Brute Force
  • Store the pointer to all the nodes of a tree in an array let say Nodes. To do this you can do a preorder traversal in the tree.
  • Now iterate through all the indices in the Nodes array. Let’s say we are currently at ith index.
    • For each index i iterate through all indices of nodes other than itself. Let's say we iterate through all indices j such that j not equal to i.
      • For each i and j, we will try to find out whether subtrees of Nodes[i] and Nodes[j] are the same or not.
      • For this, we will do a simultaneous preorder on both the nodes and if it is the same then we will return True.
  • If we don’t find any two nodes with the same subtree then we will return False.
Time Complexity

O(N ^ 3), where N is the number of nodes in the tree.

 

As for each pair of nodes, we are doing a preorder traversal.

Space Complexity

O(N) , where N is the number of nodes in the tree.

 

As we are storing pointers to all the nodes in an array.

Code Solution
(100% EXP penalty)
Check for Duplicate Subtree
Full screen
Console