Problem
Submissions
Hints & solutions
Discuss
City Lights
Hard
0/120
Average time to solve is 50m
Problem statement
Your friend Aayush is a successful businessman and earned a lot of profit this year and thought of helping out the residents of his city by renovating the old street lights of his city.
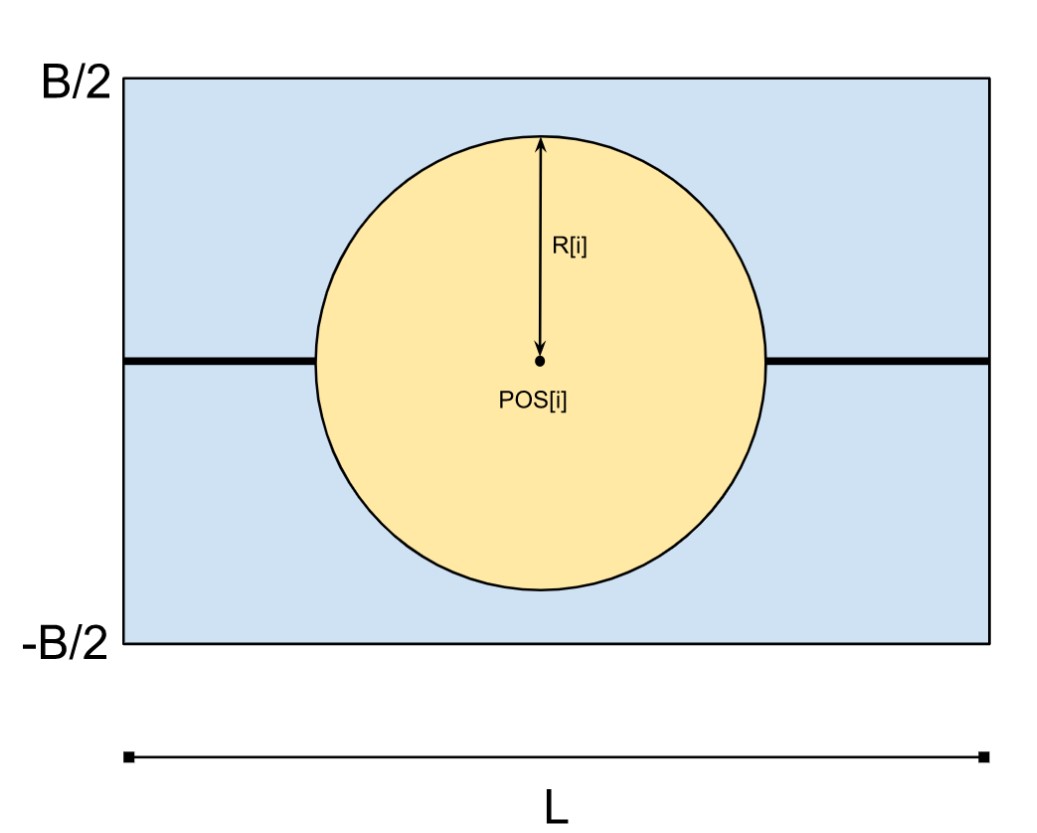
The city is a rectangle having ‘L’ as its length and ‘B’ as its breadth. The city can be imagined as a rectangular area on an X-Y plane having its left uppermost point at ‘(0, B/2)’ and right lowermost point at ‘(L, -B/2)’ (Check the image below for a better understanding).
Now in the current blueprint of the city there are ‘N’ street lights. They lie on the OX Axis if imagined in the X-Y plane whose position is given by the ‘POS’ array, all the street lights are at a distinct position. And each street light has a radius of ‘R[i]’ up to which it can illuminate the city from ‘POS[i]’.
Being a businessman Aayush decided to complete this work by replacing old street lights with new ones which will have the same position and radius as the previous street lights but with better efficiency.
But to save money and use it for other work he wanted to reduce the number of street lights to be replaced such that by replacing that many street lights the whole rectangular area of the city has the luminance of new street lights or conclude that even if he fixes all street lights there is no way the whole city can experience the luminance of new street lights.
Being his friend and a city planner Aayush asked you to help him out. Can you help him find the minimum number of street lights to be replaced such that the whole city can experience the luminance of the new street lights or print ‘-1’ if there is no way to fix the street light so that the whole area of the city can experience the luminance of new street lights?.
 .
.
NOTE: The replaced street lights should cover each and every part of the city.
EXAMPLE :Input: ‘L’ = 8, ‘B’ = 10, ‘N’ = 1, ‘POS’ = {4}, ‘R’ = {5}
Output: -1
In this case,
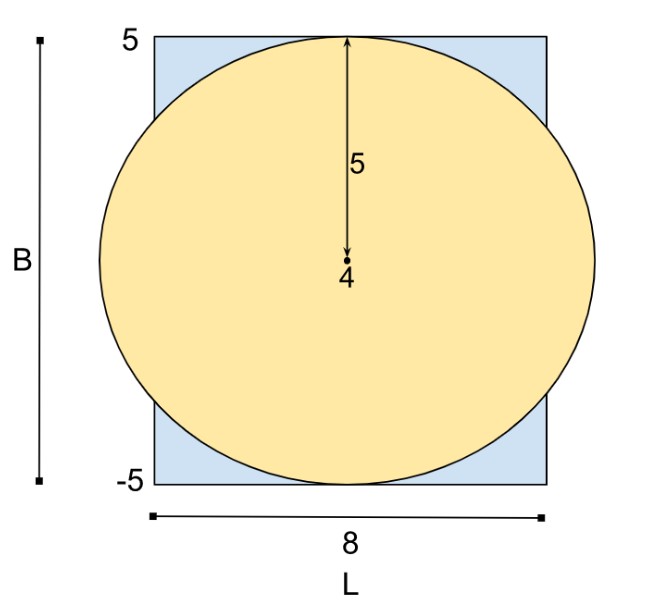
As shown in the figure above, even if we fix the only street light of the city, the whole city area can’t be covered. Hence the output is ‘-1’.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line will contain the integer ‘T’, the number of test cases.
Each test case consists of three lines.
The first line of input contains three integers, ‘L’, ‘B’, and ‘N’ separated by spaces.
The next line contains space-separated ‘N’ non-negative distinct integers, denoting the positions of the street lights in the city.
And the last line contains space-separated ‘N’ non-negative integers, denoting the radius of luminance of street lights in the city.
For each test case, print the minimum number of street lights required to illuminate the whole city with new street lights or print ‘-1’ if it is impossible to do so.
You don't need to print anything. It has already been taken care of. Just implement the given function.
Constraints :
1 <= ‘T’ <= 10
1 <= ‘N’ <= 10^5
‘N’ <= ‘L’ <= 10^5
1 <= ‘B’ <= 10^4
0 <= ‘POS[i]’ <= ‘L’
All ‘POS[i]’ are distinct, i.e. ‘POS[i] != POS[j]’ holds true for all ‘i != j’ such that ‘1’ <= ‘i’ <= ‘N’ and ‘1’ <= ‘j’ <= ‘N’
0 <= ‘R[i]’ <= 10^4
It is guaranteed that sum of ‘N’ over all test cases is <= 10^5
Time Limit: 1 sec
Sample Input 1 :
2
6 6 3
6 1 4
1 0 5
10 4 2
2 7
1 1
Sample Output 1 :
1
-1
Explanation Of Sample Input 1 :
For the first test case,
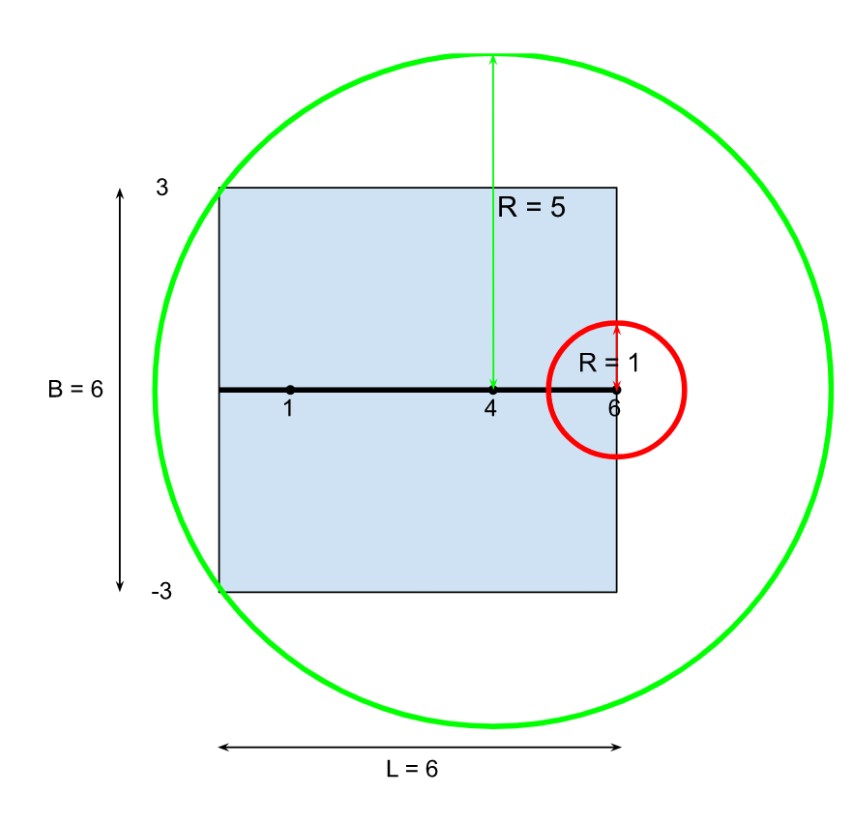
It is clearly visible, that it is advantageous to fix only the street light at position ‘4’.
Hence, the output will be: 1
For the second test case,
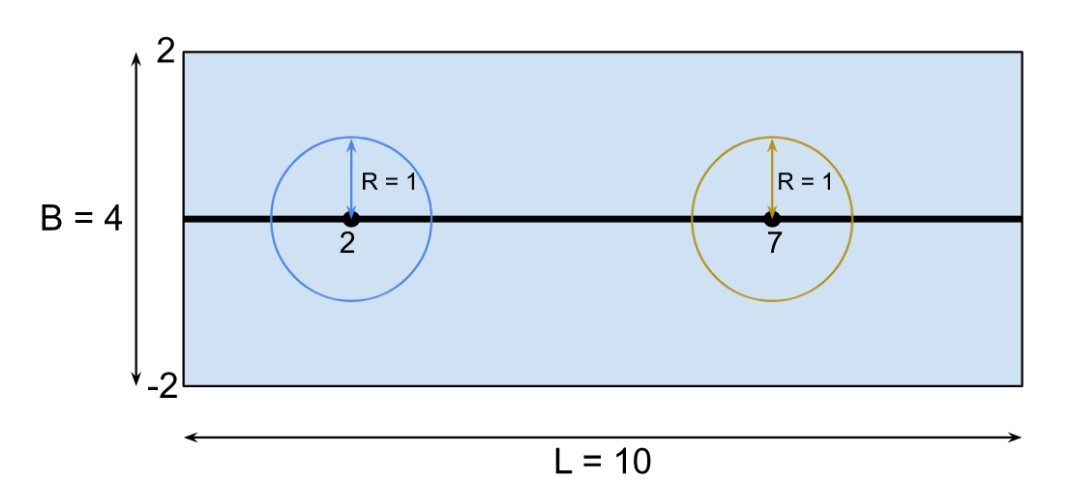
It is clearly visible, that even if we fix all the street lights of the city, we can’t have the luminance of new street lights in the whole city. Hence the output is ‘-1’
Hence, the output will be: -1
Sample Input 2 :
2
20 6 4
1 8 13 20
5 5 5 5
5 1 5
0 1 2 3 5
0 0 0 0 1
Sample Output 2 :
4
-1
Hint
Hint 1
Hint 2
Can we somehow make the area of street light luminance a function of a linear line?.
Approaches (2)
Approach 1
Approach 2
Brute Force
The idea for this approach is based on the properties of a circle.
From the above image, it is clear that if we select some street lights and the points of intersection of the circle formed by its radius and the line ‘Y = B/2’ i.e. points ‘(X1, B/2)’ and ‘(X2, B/2)’ covers the whole line segment ‘(0, B/2)’ to ‘(L, B/2)’, then each part of the city can experience the luminance of the new street lights.
Now to find ‘X1’ and ‘X2’ we can use the equation of the circle, shown in the figure.
Now for ‘Y = B/2’, the equation of the circle will be:
‘(X-P)*(X-P) + (B/2)*(B/2) = R*R’ — (1)
Now here, ‘X2 = P + D/2’
Now if we substitute the value of ‘X’ as ‘X2’ in the equation - 1, and use the above relation we get:
=> ‘(D/2)*(D/2) + (B/2)*(B/2) = R*R’, multiplying by ‘4’ both side.
=> ‘D*D + B*B = 4*R*R’
=> ‘D = SquareRoot(4*R*R - B*B)’. Let’s call ‘D/2’ as ‘V’ then,
=> ‘V = SquareRoot(4*R*R - B*B) / 2’.
=> ‘X1 = P - V’ and ‘X2 = P + V’.
And as we only have our line segment from ‘X=0’ to ‘X=L’, we can do the following modifications to values of ‘X1’ and ‘X2’.
=> ‘X1 = max(0, P - V)’ and ‘X2 = min(L, P + V)’.
Thus we can get points of intersection in this way, now after this, we have to select some subset of street lights to be fixed and check if it covers the whole line segment ‘(0, B/2)’ to ‘(L, B/2)’, if it doesn’t the answer is ‘-1’, else it’s the minimum of all possibilities.
This can be checked using a recursive algorithm in ‘O((2^N)*N)’ time complexity.
Algorithm:
// This function will check if the selected street lights cover the whole city area.
Bool isCovering(L, SELECTED, N)
- If ‘N == 0’
- Return ‘FALSE’.
- Sort the array ‘SELECTED’ in non-decreasing order of first of pair.
- Initialize a variable named ‘LEFT’ with the value of ‘0’.
- Initialize a variable named ‘RIGHT’ with the value of ‘0’.
- Run a for loop from ‘0’ to ‘N-1’ with a variable named ‘i’.
- Initialize a variable named ‘LOW’ with the value of first of ‘SELECTED[i]’.
- Initialize a variable named ‘HIGH’ with the value of second of ‘SELECTED[i]’.
- If ‘RIGHT < LOW’
- Return ‘FALSE’.
- Else
- Assign ‘RIGHT’ the value of ‘max(RIGHT, HIGH)’.
- If ‘LEFT == 0 and RIGHT == L’
- Return ‘TRUE’.
- Return ‘FALSE’.
// This function will try out every subset of street lights and find the minimum required fixing of street lights.
Void getMinimum(i, L, N, RANGE, SELECTED, &ANS)
- If ‘i == N’
- Initialize a variable named ‘SIZE’ with the value of the length of ‘SELECTED’.
- if ‘isCovering(L, SELECTED, SIZE) == TRUE’
- Assign ‘ANS’ the value of ‘min(ANS, SIZE)’.
- Return.
- Insert ‘RANGE[i]’ at the end of ‘SELECTED’.
- Call ‘getMinimum(i+1, L, N, RANGE, SELECTED, &ANS)’.
- Remove the last element of ‘SELECTED’.
- Call ‘getMinimum(i+1, L, N, RANGE, SELECTED, &ANS)’.
- Return.
// The function will return the minimum number of street lights required to be fixed.
Int cityLights(L, B, N, POS, R)
- Create an array with the name ‘RANGE’ of length ‘N’ of the type which can store real-value pairs.
- Run a for loop from ‘0’ to ‘N-1’ with a variable named ‘i’.
- Initialize a variable named ‘A1’ with the value of ‘4*R[i]*R[i]’.
- Initialize a variable named ‘A2’ with the value of ‘B*B’.
- Initialize a variable named ‘V’ with the value of ‘0’.
- If ‘A1>=A2’
- Assign ‘V’ the value of ‘squareRoot(A1 - A2) / 2’.
- Assign the first of pair ‘RANGE[i]’ the value of ‘max(0, POS[i] - V)’.
- Assign the second of pair ‘RANGE[i]’ the value of ‘min(L, POS[i] + V)’.
- Initialize a variable named ‘ANS’ with the value of ‘N+1’.
- Create an empty list ‘SELECTED’.
- Call ‘getMinimum(0, L, N, RANGE, SELECTED, ANS)’.
- If ‘ANS == N+1’
- Assign ‘ANS’ the value of ‘-1’.
- Return ‘ANS’.
Time Complexity
O((2^N)*N), Where ‘N’ is the input integer.
The number of subsets for an ‘N’ length array is ‘2^N’, and as we are iterating through each possibility there will be ‘2^N’ calls of the ‘isCovering’ function which takes O(N) time each time, hence the time complexity will be O((2^N)*N).
Space Complexity
O(N), Where ‘N’ is the input integer.
As the max recursion depth can be ‘N’ and we also use extra O(N) space for creating the ‘RANGE’ array, hence the space complexity will be O(N).
Code Solution
(100% EXP penalty)
City Lights
C++ (g++ 5.4)
Console

