Colour The Graph

Moderate
0/80
Average time to solve is 20m
profile
Contributed by
28 upvotes
Asked in companies
MeeshoChegg Inc.Microsoft

Problem statement

You are given a graph with 'N' vertices numbered from '1' to 'N' and 'M' edges. You have to colour this graph in two different colours, say blue and red such that no two vertices connected by an edge are of the same colour.

Note : 
The given graph may have connected components.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains two integers 'V' and 'E', separated by a single space. They denote the total number of vertices and edges respectively. 

From the second line onwards, the next 'E' lines represent an edge between the two vertices.

Every edge is represented by two vertices(u, v) that share an edge between them. The values of the vertices would again be separated by a single space.
Output Format : 
Print "YES" if it is possible else print "NO".
 Constraints : 
1 <= E <= 10 ^ 5
1 <= V <= 10 ^ 6

Time Limit: 1 sec
Sample Input 1 :
4 4
1 2
2 3
3 4
4 1
Sample Output 1 :
YES
Explanation for Sample 1 :
One possible coloring of the graph is:

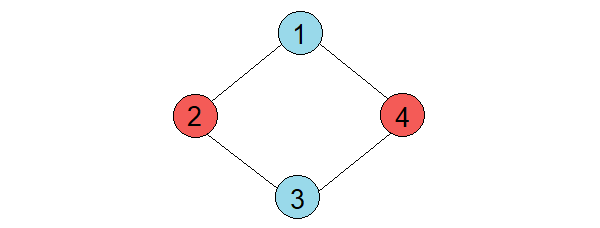
col_graph

Sample Input 2 :
3 3
1 2
2 3
3 1
Sample Output 2 :
NO
Hint

For every vertex, there are two possibilities. Either the color is Red or Blue. 

Try to explore all the possibilities by permuting the combinations of Red and Blue.

Approaches (1)
DFS

We can approach this problem by running a DFS starting from vertex-1.

We have a total of ‘m’ edges.

When can we achieve the configuration when we see in reference to vertex-1? 

  1. Let's say vertex-1 is ‘Blue’
    1. If all the vertices that connect to vertex-1 are ‘Red’, then we can say that the configuration is possible.
  2. If this would be the negation of the last one. Say, vertex-1 is ‘Red’
    1. If all the vertices that connect to vertex-1 are ‘Blue’, then we can say that the configuration is possible.

The above idea can be extended further in a Depth First manner to check the above condition on every vertex possible.

Time Complexity

O(E + V), Where E and V are the edges and vertices of the graph.

 

We are traversing through each vertex to check that no two vertices connected by an edge are of the same colour, which takes O(E + V) time. Hence, the overall Time Complexity is O(E + V).

Space Complexity

O(E), Where E is the edges of the graphs. 

 

In the worst case, we make E number of stack calls. Hence, the overall Space Complexity is O(E).

Code Solution
(100% EXP penalty)
Colour The Graph
Full screen
Console