Problem
Submissions
Hints & solutions
Discuss
Connect MidPoints
Easy
0/40
Average time to solve is 15m
15 upvotes
Asked in companies



Problem statement
You have been given a curve whose edges are parallel to either x-axis or y-axis. You need to return another curve which will pass through the midpoints of all the edges of the curve. The curve will be given in the form of a linked list, where each node represents the coordinates of the curve.
The curve to be returned will also be in the form of a linked list, where each node may represent the coordinates of the midpoints of the edges.
Note1. The coordinates of the curve will be given in non-descending order of x coordinate from start to end of the linked list and for every two adjacent coordinates either the x-coordinate or the y-coordinate will be the same.
2. All the coordinates will be pairwise distinct i.e there are no two coordinates (x1, y1) and (x2, y2) such that x1 = x2 and y1 = y2.
3. The first coordinate and the last coordinate in the input can be assumed as the starting point and the ending point of the curve respectively.
4. You may assume that the starting point and ending point of the curve will be the midpoint of the first edge, and the last edge of the input curve( in the order of input coordinates) respectively.
5. If the coordinates of the midpoint are not whole numbers, you may take the floor value of the coordinates. For example, the midpoint (3.5, 5) will be taken as (3, 5).
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains a single integer 'T' -denoting the number of test cases. Each test case consists of 4 lines as follows:
The first and the only line of each test case will contain 2 * N + 1 linked list elements (separated by space and terminated by -1), where 'N' is the total number of coordinates. Each node consists of two parts (x coordinate and y coordinate).
For example, if the input is: a1 a2 a3 a4 -1 , then the linked list is like (a1, a2) -> (a3, a4) -> NULL.
For each test case, print the coordinates of the required curve in descending order of x-coordinate. See Sample Output 1 explanation for further clarification.
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
2 <= N <= 10^4
-10^9 <= x, y <= 10^9
Time Limit: 1sec
Sample Input 1:
1
0 10 1 10 5 10 7 10 7 5 20 5 40 5 -1
Sample Output 1:
3 10 7 7 23 5
Explanation of the Sample Input1:
The curve can be represented on a x-y plane as follows:
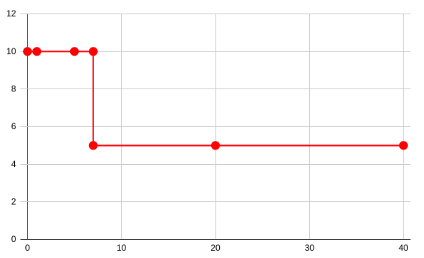
Clearly, there are two horizontal edges, and one vertical edge.
For the first edge i.e (0, 10) -> (7, 10), the midpoint will be (3, 10).
For the second edge i.e (7, 10) -> (7, 5), the midpoint will be (7, 7).
For the last edge i.e (7, 5) -> (40, 5), the midpoint will be (23, 5).
Sample Input 2:
1
1 10 1 15 -1
Sample Output 2:
1 12
Hint
Hint 1
Implementation, use midpoint formula
Approaches (1)
Approach 1
Implementation
- The fact that the edges of the curve are parallel to either of the two axes, makes this problem very trivial. We just need to calculate the coordinates of mid-points of all the edges individually and maintain the linked-list of these coordinates.
- We know that for a line segment with endpoints A(x1,y1) and B(x2, y2), the mid-point of this line will have the coordinates = M( (x1+x2)/2, (y1+y2)/2) ) .
- Thus we will try to form a line segment between every two consecutive edges, and then all the lines together will be our required curve
- We create a new empty linked list, and have a dummy pointer pointing towards the start of this list.
- Then what we need to do is simply store the starting point of an edge, and as long as we are moving in the same direction i.e either horizontally( if two adjacent coordinates have same y-coordinate) or vertically ( if two adjacent coordinates have same x-coordinate), we keep on updating the end point of that edge.
- When we find the endpoint , the mid point is simply calculated using the above mentioned formula and a node is added to the new linked list with coordinates of this mid-point.
- Note- In most programming languages(C, C++, Java), the integer division (or the normal division) results in the floor value, so the problem of decimal coordinates will be already taken care of in these languages. However this is not the case in languages like Python , as these languages carry out floating point divisions.
Time Complexity
O(N) , where N is the number of coordinates in the input.
As we are processing each coordinate only once, thus the total complexity will be proportional to the total number of coordinates.
Space Complexity
O(1), as we are using constant extra space.
Code Solution
(100% EXP penalty)
Connect MidPoints
Javascript (node v10.20.0)
Console
