Problem
Submissions
Hints & solutions
Discuss
Critical and Pseudo-Critical Edges
Hard
0/120
Average time to solve is 50m
Problem statement
You are given a weighted undirected connected graph with ‘n’ vertices numbered from 0 to (n - 1), and array 'EDGES' where EDGES[i] = [ ai, bi, WEIGHT ] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.
Your task is to find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.
Note:
1) A weighted graph refers to one where weights are assigned to each edge, undirected graphs are those where edges are bi-directional and have no arrows.
2) If no edge exists return -1.
3) Return the edges in the sorted order of their indices.
For example:
N = 4, M = 4
[[0, 1, 1],
[0, 2, 1],
[0, 3, 2],
[2, 3, 2]]
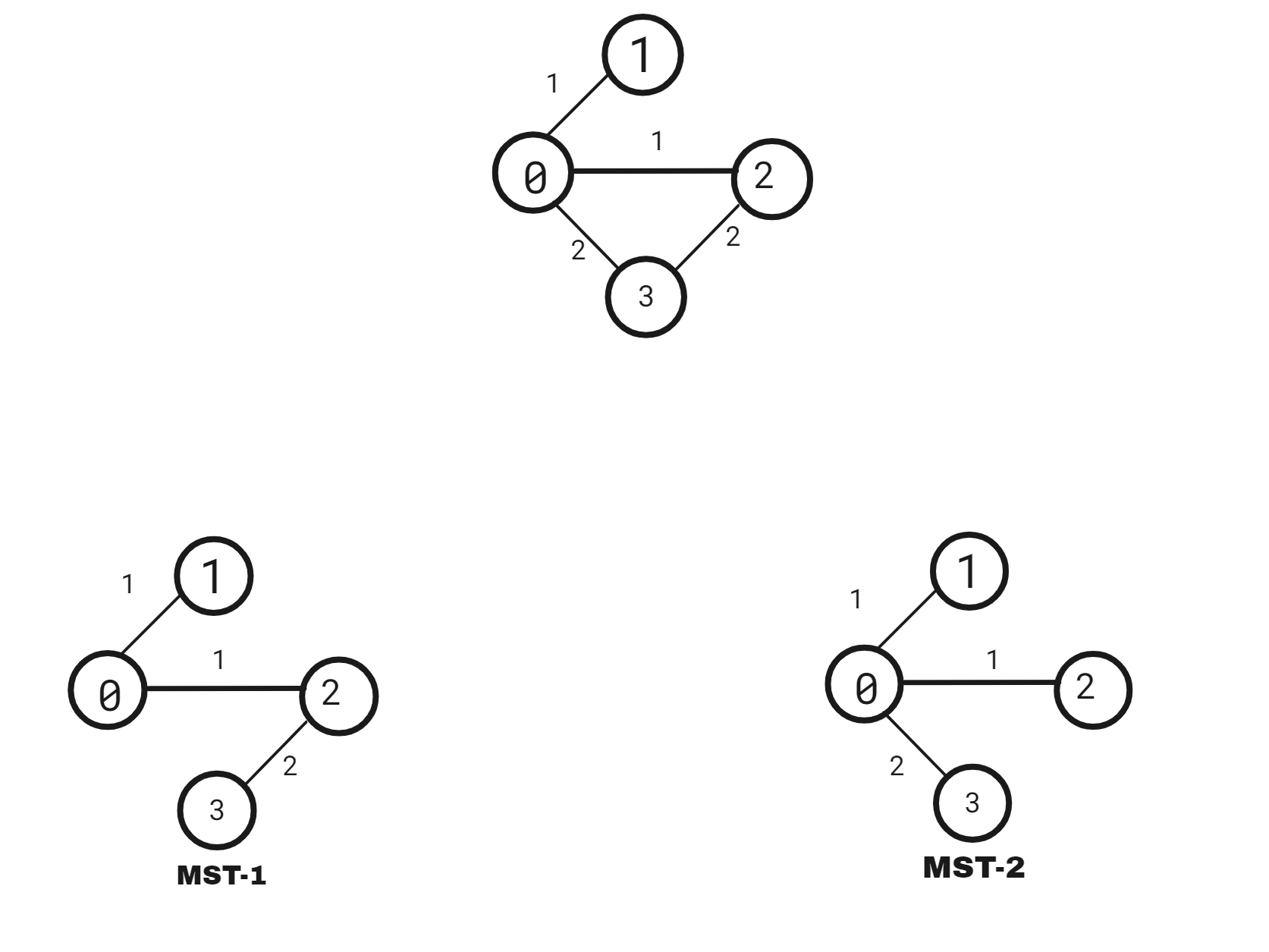
The critical connections are the 0th connection and the 1st connection because removing the causes the MST weight to increase.
The 2nd and 3rd connections are pseudo-critical because any one of the edges can be taken to make MST.
Detailed explanation ( Input/output format, Notes, Images )
Input format:
The first line of input contains an integer T denoting the number of test cases.
The first line of each test case contains exactly two space-separated integers, ‘N’, which denotes the number of nodes, and ‘M’, which denotes the number of edges.
The next 'M' lines contain exactly three space-separated integers representing 'NODE1', 'NODE2', and 'EDGE WEIGHT'.
Output format:
For each test case, print single lines containing two space-separated integers for each pseudo-critical connections and the critical connection. If any of this doesn’t exist return -1.
The output of each test case will be printed in a separate line.
Note:
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 5
1 <= N <= 500
1 <= M <= 1000
0 <= EDGES[i][j] <= 10^5
Where ‘T’ is the total number of test cases, 'N' is the number of nodes and 'M' is the number of edges, ‘EDGES’ is the given matrix and ‘EDGES’[i][j] is the value of pairs (i,j).
Time limit: 1 sec
Sample Input 1 :
2
4 4
0 1 1
0 2 1
0 3 2
2 3 2
3 3
0 1 2
2 0 1
1 2 1
Sample Output 1:
0 1
2 3
1 2
-1
Explanation Of Sample Input 1:
For the first test case:

The critical connections are the 0th connection and the 1st connection because removing the causes the MST weight to increase.
The 2nd and 3rd connections are pseudo critical because any one of the edges can be taken to make MST.
For the second Test case :
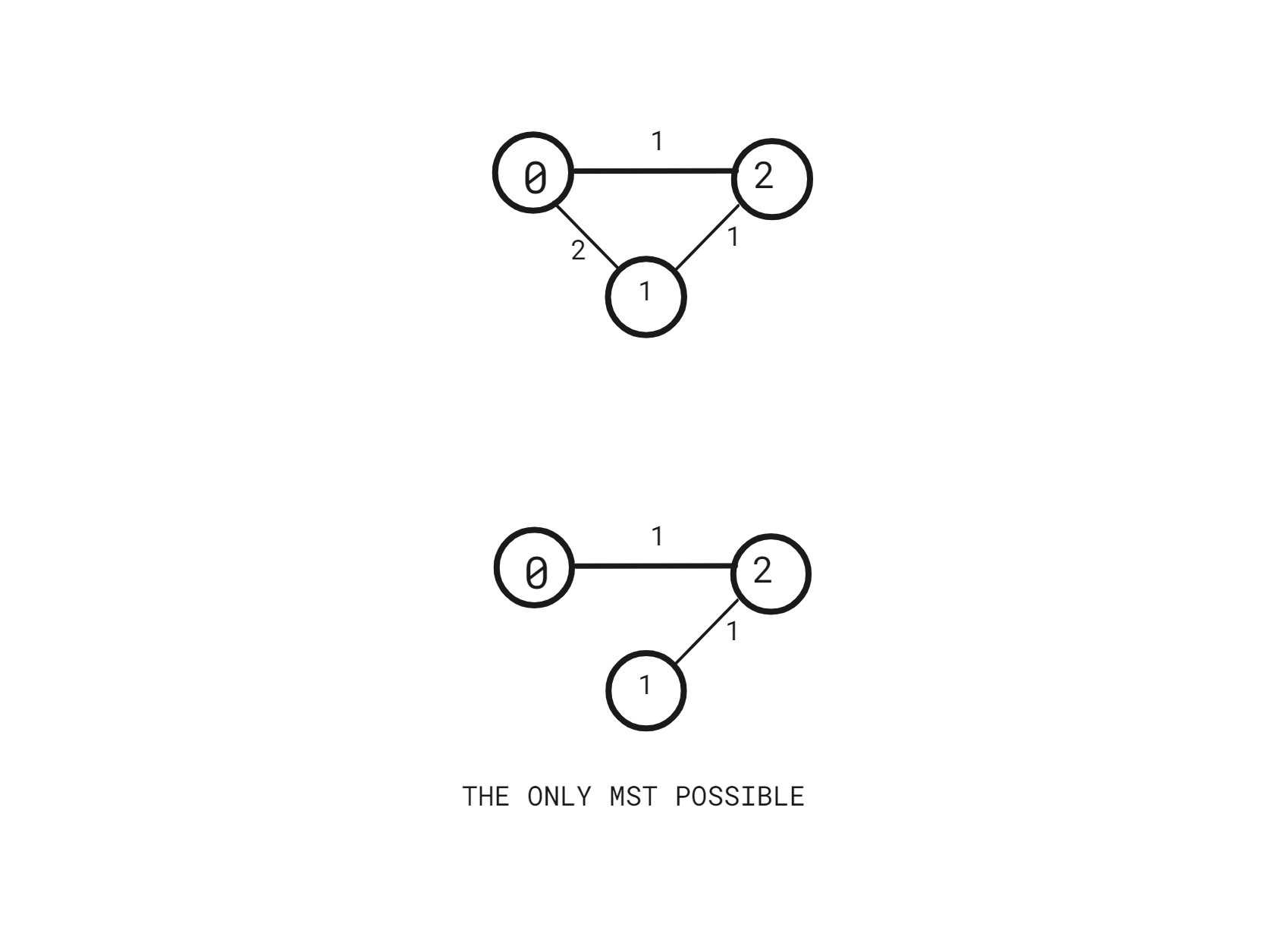
Edge 1 and 2 are critical for the formation of a minimum spanning tree.
There is no other edge that is required for the formation of MST, hence there is no pseudo-critical connection, therefore we returned -1.
Sample Input 2 :
2
4 4
0 1 1
1 2 1
2 3 1
0 3 1
5 7
0 1 1
1 2 1
2 3 2
0 3 2
0 4 3
3 4 3
1 4 6
Sample Output 2 :
-1
0 1 2 3
0 1
2 3 4 5
Hint
Hint 1
Can you find the connected components using DSU?
Approaches (1)
Approach 1
DSU
The main idea is to use a DSU data structure, to find connected components. A DSU data structure can be used to maintain knowledge of the connected components of a graph, and query for them quickly. In particular, we would like to support two operations:
find(node x), which outputs a unique id so that two nodes have the same id if and only if they are in the same connected component, and:
union(node x, node y), which draws an edge (x, y) in the graph, connecting the components with id find(x) and find(y) together.
Using DSU we need to find MST, using the Kruskal algorithm.
Below are the steps for finding MST using Kruskal’s algorithm
- Sort all the edges in non-decreasing order of their weight.
- Pick the smallest edge. Check if it forms a cycle with the spanning-tree formed so far. If the cycle is not formed, include this edge. Else, discard it.
- Repeat step number 2 until there are (V-1) edges in the spanning tree, where V is the number of vertices.
- We use the standard MST algorithm as a baseline and find the minimum weight of the MST i.e. ‘minWt’, which we would compare with the new trees that will be formed to check if they are MST’s.
- To generate critical and pseudo-critical lists, we enumerate each edge and for the ‘i’th edge :
- We traverse all edges and don’t consider the ‘i’th edge.
- Then re-calculating the MST again makes MST total weight increase (or can't form MST), then the edge goes into the critical list.
- If we force adding the edge to the MST (by first adding the edge to the MST edge set and run the standard MST algorithm for the rest of the edges) and find that the MST doesn't change, then the edge goes into the pseudo-critical list. This is because if an edge can be in any MST, we can always add it to the edge set first, without changing the final MST total weight.
- Finally, we return ‘critical’ and ‘pseudoCritical’ vectors as the result.
Time Complexity
O( M ^ 2 ), where ‘M’ is the number of edges.
Since for every edge we considered for making the MST, we will one by one remove the considered edge and try to replace it with the unused edges, Therefore O(M * M) = O(M ^ 2 ).
Space Complexity
O(N * M), where ‘N’ is the number of nodes, ‘M’ is the number of edges.
Since for every edge, we check all other edges, Therefore for every iteration, we will store the parent array therefore the net space complexity will be O(N * M).
Code Solution
(100% EXP penalty)
Critical and Pseudo-Critical Edges
C++ (g++ 5.4)
Console



