Problem
Submissions
Hints & solutions
Discuss
Conquer the Best Kingdom
Moderate
0/80
Problem statement
Aragorn is a great ruler and desires to become the most powerful in the entire world. There are ‘N’ kingdoms, kingdoms are numbered from 0 to 'N' - 1 and form of a tree, you are also given the information about the edges of this tree depicting all the Kingdoms that are adjacent to each other.
The ruler with the most kingdoms is considered the most powerful. You desire to become the greatest ruler without having to fight with Aragorn. Kingdoms are conquered one at a time in turns in order to make the process smooth and less violent.
Aragorn initially rules only the ‘Xth’ kingdom and all other kingdoms are not ruled by anyone. In each turn, a ruler can conquer another kingdom that is adjacent to one of his current kingdoms and is ruled by none of the rulers, the opponent plays the next turn and the process is repeated. The game continues until both the players run out of moves. If a ruler has no available adjacent kingdom to conquer then he passes his turn. In the end, the ruler with more kingdoms under his control wins the game.
Aragorn gives you an advantage in the first turn, letting you choose a kingdom of your choice, but for all other moves, you can only conquer a kingdom adjacent to one of your current kingdoms. If Aragorn plays optimally, determine if it’s possible for you to win by becoming the most powerful or not, print “true” if you can become more powerful than Aragorn, else return “false”.
For Example :If N = 7, X = 2 and Edges = { {0, 1}, {0, 2}, {1, 4}, {1, 5}, {2, 3}, {4, 6} }
Then the tree is:
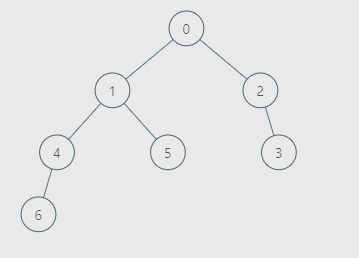
Here N = 7 depicts that there are seven kingdoms (numbered from 0 to 6). Edges depict that kingdom-0 and kingdom-1 are adjacent, kingdom-0 and kingdom-2 are adjacent, and so on. And Aragorn initially controls kingdom-2.
Then in this case, if you select kingdom-1 in your first then, then Aargon will select kingdom-0 in the next turn, as both rulers play optimally, therefore in the end Aargon will be ruling kingdom-0, kingdom-2 and kingdom-3 and the remaining four kingdoms will be ruled by you. Hence you will be able to win the game and therefore we will print “true”.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line contains a single integer ‘T’ denoting the number of test cases, then each test case follows:
The first line of each test case contains three integers ‘N’, and ‘X’ denoting the number of kingdoms and the kingdom initially ruled by Aragorn respectively.
The next N - 1 lines each contain two integers each denoting the kingdoms that are adjacent to each other.
For each test case, print “true” if you can conquer more kingdoms than Aragorn, else print “false”.
Output for each test case will be printed in a separate line.
You are not required to print anything; it has already been taken care of. Just implement the function.
Constraints :
1 ≤ T ≤ 10
2 ≤ N ≤ 1000
0 ≤ X < N
0 ≤ Edges[i][0], Edges[i][1] < N
Time limit: 1 sec
Sample Input 1 :
2
7 2
0 1
0 2
1 4
1 5
2 3
4 6
2 0
0 1
Sample Output 1 :
true
false
Explanation For Sample Input 1 :
For test case 1 :
We will print “true” because:
You can conquer kingdom-1 in your first turn, this will finally result in Aragorn controlling kingdom-0, kingdom-2 and kingdom-3 and all other kingdoms will be controlled by you.
For test case 2 :
We will print “false” because:
Aragorn initially controls kingdom-0, as there are only two kingdoms so you will conquer kingdom-1 in your turn, the game will end after this. In the end, you don’t have more kingdoms than Aragorn, therefore you can’t become more powerful than Aragorn.
Sample Input 2 :
2
4 0
0 1
0 2
0 3
7 0
0 1
0 2
0 3
3 4
4 5
5 6
Sample Output 2 :
false
true
Hint
Hint 1
Figure out why the first kingdom you select will solely determine the final answer.
Approaches (1)
Approach 1
Greedy + Depth First Search
The question becomes easy if you are able to figure out that only the decision of selecting the first kingdom to conquer will be sufficient to determine the final answer. Let’s start with something more intuitive rather than directly jumping to the final answer. If you pick a random kingdom in your first turn, in subsequent turns both you and Aragorn you will greedily conquer all the kingdoms that lie on the shortest path connecting the kingdom-X (initially ruled by Aragorn) and the random kingdom that you decide to conquer in your first turn. This happens because both of you play optimally, so both the rulers will try to decrease the number of kingdoms that the other may conquer in future, this is simply done by blocking the kingdoms that are between both the initially conquered kingdoms. Therefore by selecting a random kingdom we can determine who will win finally.
Now extending this logic further, selecting a random kingdom in the beginning gives the other player (Aragorn) the opportunity to conquer the kingdoms that lie between the initial kingdoms. We can easily remove this possibility by conquering a kingdom that is just adjacent to Aragorn’s initial kingdom. In this way, we can greedily find if it is possible for us to win, as the kingdom we initially select will make sure that we can conquer the entire subtree of that initial kingdom in future, as all the kingdoms form a tree and there would be no cycles, so Aragorn would never be able to conquer any kingdom that lies in the subtree of our initial kingdom, on the same note we would also never be able to conquer any other kingdom that doesn’t lie in the subtree of our initial kingdom.
To implement this logic, Apply depth-first search on every adjacent kingdom of X, make sure that Xth node is not visited in dfs. Find out the subtree with the maximum number of nodes. Finally, check if the subtree with the most number of nodes has more than half the total kingdoms, then print “true” else we will print “false”.
The steps are as follows :
- Declare ‘adj’ to store the given tree in form of an adjacency list. Fill the adjacency list using ‘Edges’.
- Created a ‘vis’ array to keep track of the conquered kingdoms. Mark vis[X] equal to 1.
- Traverse all the adjacent nodes of ‘X’ in the adjacency list, and apply depth-first search on each of them to calculate the total number of nodes in their respective subtrees. Use a variable ‘mxSubtree’ to store the maximum size of the subtree calculated.
- Finally, return “true” if ‘mxSubtree’ is greater than N / 2, else return “false”.
Time Complexity
O( N ), where N denotes the number of kingdoms.
We visit each kingdom exactly once, as the number of kingdoms is equal to N.
Hence the time complexity is O( N ).
Space Complexity
O( N ), where N denotes the number of kingdoms.
We create an adjacency list to store the information of the tree so that we can implement the dfs easily. Information about all the N - 1 edges is stored in this list.
Hence the space complexity is O( N ).
Code Solution
(100% EXP penalty)
Conquer the Best Kingdom
C++ (g++ 5.4)
Console



