Constellation

Easy
0/40
Average time to solve is 10m
profile
Contributed by
9 upvotes
Asked in company
Samsung R&D Institute

Problem statement

Given a matrix ‘UNIVERSE’ with 3 rows and ‘N’ columns, with the characters { # , * , . } and these characters represent a cluster of stars and galaxies in space. Stars are represented by ‘*’ symbol. The ‘.’ symbol represents empty space.


We define a constellation as a 3x3 matrix which contains stars in the shape of vowels. A group of constellations is defined as a galaxy. Note that a galaxy may contain many stars but they will never be overlapping. Two galaxies are separated by a column of ‘#’.


Given the ‘UNIVERSE’ matrix, print a string which denotes all the vowels formed by stars and ‘#’ present in the matrix.


A looks like this : 
. * .
* * *
* . *
E looks like this : 
* * *
* * *
* * *
I looks like this : 
* * *
. * .
* * *
O looks like this : 
* * *
* . *
* * *
U looks like this : 
* . *
* . *
* * *


Note : 
It is guaranteed that no two constellations are overlapping.


Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line of input contains an integer ‘T’ denoting the number of test cases.

The first line of each test case contains a single integer ‘N’ denoting the number of columns in the matrix.

The next 3 lines of each test case denote the matrix of size 3 rows and ‘N’ columns which denotes the stars and the galaxies. Each line contains ‘N’ space separated characters from the set { ‘#’ , ’*’ , ’.’ }.


Output format : 
For each test case, print a string which contains the shape of vowels and the hashes.


Note : 
You do not need to print anything, it has already been taken care of. Just implement the given function.


Constraints: 
1 <= T <= 50
3 <= N <= 10^5

Time Limit: 1 sec
Sample Input 1 :
2
12
* . * # * * * # * * * # 
* . * # * . * # . * . # 
* * * # * * * # * * * # 
7
* * * # * * *
* * * # * . *
* * * # * * *
Sample Output 1 :
U#O#I#
E#O
Explanation For Sample Input 1 :
For the first test case,


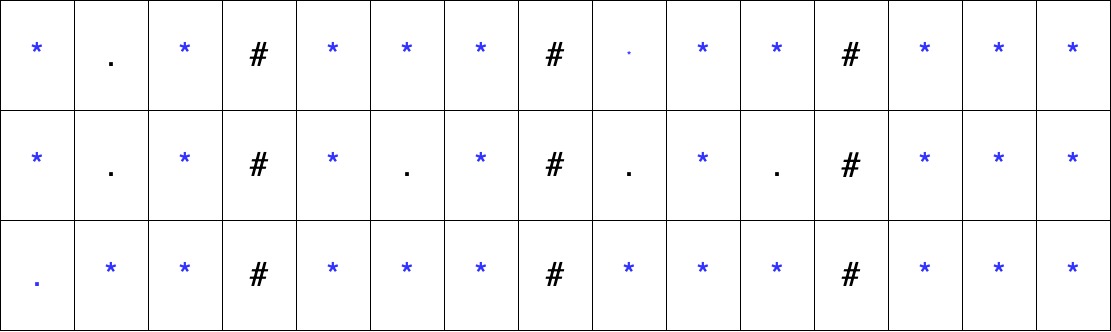
We can clearly make out the blue U O I and E the A is in red to differentiate from E.

For the second test case,


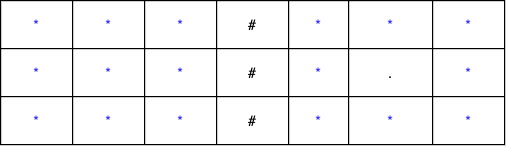
We can clearly see the E and O in blue
Sample Input 2 :
2
11
* * * # * * * # * . *
* * * # . * . # * . *
* * * # * * * # * * * 
3
* * *
* . *
* * *
Sample Output 2 :
E#I#U
O
Hint

Check alphabet in every 3x3 grid recursively.

Approaches (2)
Recursive Approach

The key idea is to recursively check every 3x3 grid and see what vowel does it signify and it to the string. This can be easily done using a recursive function.

 

Here is the algorithm :

 

  1. We take a recursive function ‘generateConstellations()’ and take parameters, ‘CURIDX’, which denotes the current column we are at, a matrix ‘UNIVERSE’ to denote the stars and constellations.
  2. We define ‘MAT’ as submatrix of size 3x3 of the matrix ‘UNIVERSE’.
  3. We append the string ‘STR’ with the following conditions.
  4. If it is an ‘A’ the MAT[0][1], MAT[1][0], MAT[1][1], MAT[1][2], MAT[2][0] and MAT[2][2] will be stars.
  5. If it is an ‘E’ all elements of the matrix will be stars.
  6. If it is an ‘I’ all elements except MAT[1][0] and MAT[1][2] will be stars
  7. If it is an ‘O’ all elements except MAT[1][1] will be stars
  8. If it is an ‘U’ all elements except MAT[0][1] and MAT[1][1] will be stars.
  9. If it is a ‘#’ all 3 rows of that column will be ‘#” and we append ‘#’ to our string ‘STR’.
  10. Check every 3x3 matrix at a time and add the vowel formed to the resultant string ‘STR’.
  11. The base case will be once we have traversed the whole string i.e ‘CURIDX’ is greater than equal to N-2.
  12. Finally, when the whole matrix is traversed, return ‘STR’.
Time Complexity

O(N), where ‘N’ denotes the number of columns in the matrix.

 

We need to traverse each column once hence the overall time complexity will be O(N).

Space Complexity

O(N), Where ‘N’ denotes the number of columns in the matrix.

 

Recursive stack uses space of order of ‘N’. Therefore, the overall space complexity will be O(N).

Code Solution
(100% EXP penalty)
Constellation
Full screen
Console