Problem
Submissions
Hints & solutions
Discuss
Contain Virus
Hard
0/120
Average time to solve is 45m
10 upvotes
Asked in companies



Problem statement
With every passing night, the virus spreads to all the adjacent cells, unless the cells are blocked by a wall. You need to build walls in order to stop the virus from spreading in the whole country. Note that you can only install walls around only one region which is the affected area that threatens to infect the most uninfected cells of the matrix in one day.
Given the state of each cell, your task is to find the number of walls you used to stop as many cells as possible from being infected.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains an integer ‘T’ which denotes the number of test cases or queries to be run. Then the test cases are as follows.
The first line of each test case contains two space-separated integers ‘N’ and ‘M’, denoting the dimensions of the country model.
Each of the next ‘N’ lines contains ‘M’ elements each denoting the state of the cell.
For each test case, print a single line containing a single integer denoting the number of walls required.
The output of each test case will be printed in a separate line.
You don’t need to print anything; It has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
1 <= N, M <= 100
0 <= X <= 1
Where ‘T’ is the number of test cases, ‘N’ and ‘M’ denotes the dimensions of the model, ‘X’ denotes the element of the matrix.
Time limit: 1 sec.
Sample Input 1:
2
3 3
1 1 1
1 0 0
1 1 1
3 9
1 1 1 0 0 0 0 0 0
1 0 1 0 1 1 1 1 1
1 1 1 0 0 0 0 0 0
Sample Output 1:
5
13
Explanation of sample input 1:
In the first test case, we can see in the above model, in order to save the uninfected cells from getting infected, we would require 5 walls.
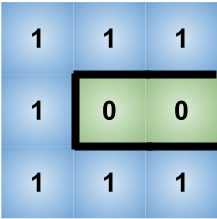
In the second test case, we can see in the model, in order to save the uninfected cells from getting infected, we would require 13 walls.
.png)
Sample Input 2:
2
2 2
1 0
0 0
3 3
1 1 1
1 0 1
1 1 1
Sample Output 2:
2
4
Hint
Hint 1
Can you think of using Depth First Search to solve the problem?
Approaches (1)
Approach 1
Depth First Search
The approach is to get clusters of infected areas in each step. Deal with the largest cluster and expand the rest of the clusters.
Let us understand this using an example:
INPUT:
1 1 1 0 0 0 0 0 0
1 0 1 0 1 1 1 1 1
1 1 1 0 0 0 0 0 0
First iteration:
The highlighted area is the largest cluster as it infects the most cells. So, we will make walls around this area, in this case 11 walls and make the neighbors infected for the other infected area.
Second Iteration:
The highlighted area now is the largest cluster and the only cluster left in this case. So, make walls around the area, in this case 2 walls that touch the non-infected area.
Now, there are no more infected areas that can infect the cells. So, return the number of walls used, in this case 11 + 2 = 13 walls.
Algorithm:
- To start with, we will create a class “Cluster”, consisting of a set of cells that are infected, a set of cells that are next to this cell and are not infected, and the count of walls required to contain this structure. This class will be used for all the clusters.
- In the main function, create a visited matrix and initialise a variable “ans” = 0.
- Now, search for the infected cell in the given model using DFS.
- Create a cluster for every value and apply DFS.
- For DFS, create a recursive function:
- If the current cell is out of model bounds or if the cell is already visited or if the current cell is already blocked by a wall, then we will simply return.
- If the cell is not infected then add it to the set of not infected cells and increment the wall count.
- Otherwise, add it to the set of infected cells and mark it as visited.
- Finally call DFS in all the directions of the infected cells.
- Get the biggest cluster by finding the cluster with the maximum number of non-infected adjacent cells out of all the created clusters, Make all cells belonging to the biggest cluster as -1 and add the number of required walls to contain them, and add them to “ans”, the variable used to store the total number of walls required.
- For the rest of the clusters make their not infected cells as infected.
- Return ans.
Time Complexity
O((N * M) ^ 4/3), where N and M are the dimensions of the model.
Since the size of infected region with respect to time ‘T’ is (T ^ 2) and after every passing time, the infected area decreases, so we can expand this expression as: T ^ 2 + (T - 1) ^ 2 + (T - 2) ^ 2 and so on…, which is equal to 1/6 * T(2*T ^ 2 + 3*T + 1), which means, for number of iterations required can be approximated as T ^ 3 <= N * M, which gives an upper bound for T = ((N * M) ^ ⅓) iterations and for every iteration it takes O(N * M) time. Hence, the overall time complexity of the above approach will be O((N * M) ^ 4/3).
Space Complexity
O(N * M), where N and M are the dimensions of the model
The space required for the sets is O(N * M), so the overall complexity will be O(N * M).
Code Solution
(100% EXP penalty)
Contain Virus
C++ (g++ 5.4)
Console
