Container With Most Water

Moderate
0/80
Average time to solve is 15m
85 upvotes
Asked in companies
MicrosoftAmazonSAP Labs

Problem statement

Given a sequence of ‘N’ space-separated non-negative integers A[1],A[2],A[3],......A[i]…...A[n]. Where each number of the sequence represents the height of the line drawn at point 'i'. Hence on the cartesian plane, each line is drawn from coordinate ('i',0) to coordinate ('i', 'A[i]'), here ‘i’ ranges from 1 to ‘N’. Find two lines, which, together with the x-axis forms a container, such that the container contains the most area of water.

Note : 
1. You can not slant the container i.e. the height of the water is equal to the minimum height of the two lines which define the container.

2. Do not print anything, you just need to return the area of the container with maximum water.
Example

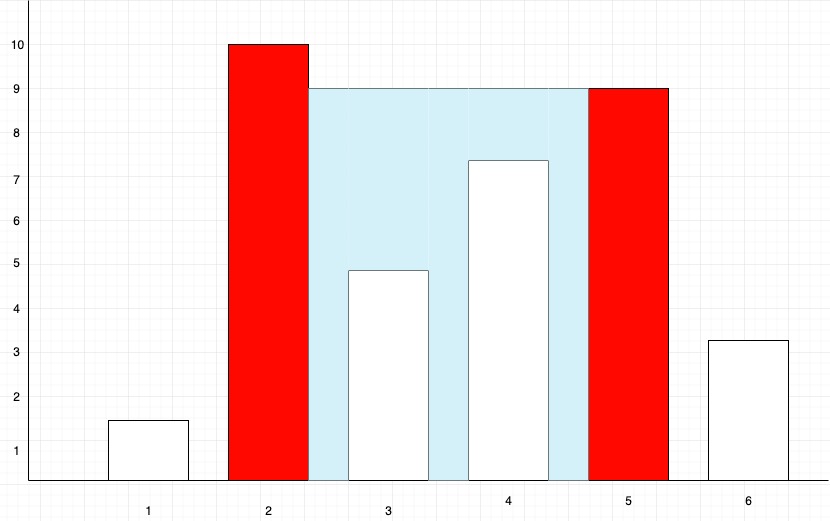
water-diagram

For the above Diagram, the first red marked line is formed between coordinates (2,0) and (2,10), and the second red-marked line is formed between coordinates (5,0) and (5,9). The area of water contained between these two lines is (height* width) = (5-2)* 9 = 27, which is the maximum area contained between any two lines present on the plane. So in this case, we will return 3* 9=27.
Detailed explanation ( Input/output format, Notes, Images )
Input format : 
The first line of input contains an integer ‘T’ denoting the number of test cases.

The next ‘2*T’ lines represent the ‘T’ test cases.

The first line of each test case contains the number of elements in the sequence.

The second line of each test case contains ‘n’ space-separated integers which is the given sequence.
Output format : 
For every test case return the area of the container which can hold the maximum amount of water using any pair of lines from the given sequence.
Constraints: 
1 <= T <= 50
0 <= N <= 10^4
1 <= A[i] <= 10^5

Time Limit: 1 sec
Sample Input 1 :
2
5
4 3 2 1 4
3
1 2 1
Sample Output 1 :
16
2
Explanation of The Sample Input 1:
For the first case: 
We can create ‘n(n+1)/2’ different containers using ‘N' containers for example with 1st and 3rd line we can create a container of area = (3-1)*min(4,2)=4.

All Possible Containers:  


Lines used          Area
4,3         area=min(4,3)*1=3
4,2         area=min(4,2)*2=4
4,1         area=min(4,1)*3=3
4,4         area=min(4,4)*4=16
3,2         area=min(3,2)*1=2
3,1         area=min(3,1)*2=2
3,4         area=min(3,4)*3=9
2,1         area=min(2,1)*1=1
2,4         area=min(2,4)*2=4
1,4         area=min(1,4)*1=1


But among all such containers the one with the maximum area will be formed by using the first and last line, the area of which is : (5-1)*min(4,4)=16.

Hence we return 16.

For the second case: 
We can take the first and third line to get an area of (3-1)*min(1,1)=2 which is the maximum possible area in this sequence.
Sample Input 2 :
2
5
12 4 6 8 1
3
1 2 3
Sample Output 2 :
24
2
Hint

Try to find the area of all possible containers and choose maximum.

Approaches (2)
Brute Force Approach

Since we need to find the container with most water, let us try to find all possible containers and choose the one which has the maximum area.

So how can we find the area of all possible containers?

We can, for each line with the position ‘i’ find another line ‘j’ such that ‘j’ > ‘i’ and find the amount of water contained i.e (‘j’-’i’)*min('A[i]', ‘A[j]’) where ‘A[i]’ and ‘A[j]’ represents the height of the lines at index ‘i’ and ‘j’ respectively.

We can do this in the following way:

  • Take a variable ‘GLOBAL_MAX' to store the overall maximum area and initialize it to some very small value (eg -1).
  • Let ‘N’ be the number of lines in the sequence.

 

  • Let ‘HEIGHT[i]’ be the height of the first line of any container. Then for each ‘i’ we find ‘HEIGHT[j]’ where ‘i’<j<’N-1’ which is the height of the second line for the container. We compute its current area in a variable ‘CURRENT_AREA’ which is (j-i)*min(A[j], A[i]) and compare with the maximum area i.e ‘GLOBAL_MAX’  achieved till now. If the ‘CURRENT_AREA’ is greater than ‘GLOBAL_MAX’ we update the maximum area.
  • In the end, we return the value of ‘GLOBAL_MAX’.
Time Complexity

O(N^2), Where ‘N’ denotes the number of elements in the given sequence.  

 

For each starting height, we calculated the area for the container. This is done for all ‘N’ lines in the container and in the worst case, this is done ‘N’ times. Hence the complexity is of order  O(N^2).

Space Complexity

O(1), 

 

We are using constant space.

Code Solution
(100% EXP penalty)
Container With Most Water
Full screen
Console