Problem

Submissions

Hints & solutions

Discuss

Convert Min Heap To Max Heap

Moderate

0/80

Average time to solve is 25m

15 upvotes

Asked in companies

Problem statement

You are given an array of size ‘N’ which is an array representation of min-heap.

You need to convert this min-heap array representation to a max-heap array representation. Return the max-heap array representation.

For Example

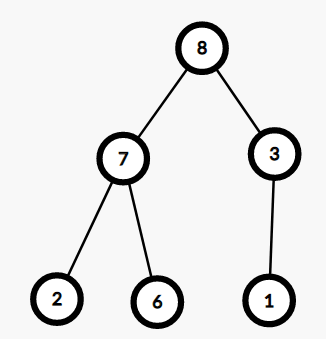
Corresponding to given min heap : [1,2,3,6,7,8]

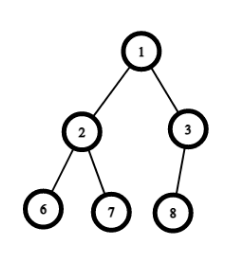
It can be converted to the following max heap: [8,7,3,6,2,1]

Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line contains a single integer ‘N’ denoting the size of the array.

The next line contains ‘N’ space-separated integers denoting the array representation of min-heap.

Output Format

There can be many possible max-heaps. Return any possible max-heap for given input min-heap.

Sample Input 1 :

6
1 2 3 4 5 6

Sample Output 1:

true

Explanation to Sample Input 1:

The min-heap representation is:-

One of the possible max heap for a given min-heap 
is [6,5,4,2,3,1]

Sample Input 2:

7
3 5 6 7 9 12 7

Sample Output 2:

true

Constraints:

1 <= ’N’ <= 5000
1 <= arr[ i ] <= 10^5

where, 'N' denotes the size of the array and arr[i] denotes the elements of the input array.

Time Limit : 1 sec

Hint 1

Hint 2

Sort the array in descending order.

Approaches (2)

Approach 1

Approach 2

Sorting Approach

The main idea is that when an array is sorted in descending order it becomes max heap as for every ‘i’ from i=0 to n/2 it is greater than equal to arr[2*i+1] and arr[2*i+2].

Time Complexity

O(n*log(n)), where n is the size of the array.

Sorting an array takes O(n*log(n)) time complexity.

Space Complexity

O(1)

We are using constant space to solve this.

(100% EXP penalty)

Convert Min Heap To Max Heap

Console