Problem
Submissions
Hints & solutions
Discuss
Convert Sorted Array to BST
Easy
0/40
Average time to solve is 15m
Problem statement
You have been given a sorted array of length ‘N’. You need to construct a balanced binary search tree from the array. If there can be more than one possible tree, then you can return any.
Note:
1. A balanced binary tree is a binary tree structure in which the left and right subtrees of every node differ in height by no more than 1.
2. A binary search tree is a binary tree data structure, with the following properties
a. The left subtree of any node contains nodes with value less than the node’s value.
b. The right subtree of any node contains nodes with values equal to or greater than the node’s value.
c. Right, and left subtrees are also binary search trees.
Example:
Below tree, is a balanced binary search tree
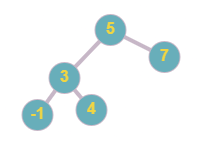
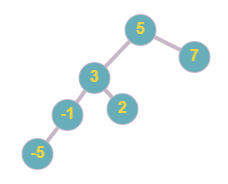
Below tree is not a balanced tree as the height of the left subtree and right subtree of node ‘5’ differs by more than 1. Moreover, the tree is also not a BST as node ‘2’ is less than node ‘3’ but ‘2’ is the right child of ‘3’.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains an integer 'T' which denotes the number of test cases or queries to be run.
The first line of each test case contains an integer ‘N’ which denotes the number of elements in the array.
The second line of each test case contains ‘N’ space-separated integers denoting the elements of the array in strictly increasing order.
Output Format:
For each test case, the output will be “1” if you have returned the correct answer, else it will be “0”.
Note :
You do not need to input or print anything, and it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 5
1 <= N <= 3000
1 <= arr[i] <= 10 ^ 5
Where 'arr[i]’ is the value of i-th element of the given array
arr[0] < arr[1] < arr[2] . . . < arr[N].
Time Limit: 1 sec
Sample Input 1:
2
5
1 2 3 4 5
1
12
Sample Output 1:
1
1
Explanation of Sample Input 1:
For the first test case, one of the possible balanced BST will look like.
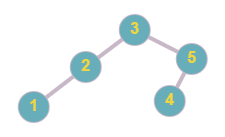
Level order traversal of the above tree is [ 3, 2, 5, 1, -1, 4 ], if you return this tree then you will get the output as 1.
For the second test case, the tree has only one node that is ‘12’.
Level order traversal is [ 12 ], if you return this tree then you will get the output as 1.
Sample Input 2:
1
2
5 17
Sample Output 2:
1
Explanation of Sample Input 2:
The tree will look like this.
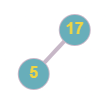
Another possible tree is
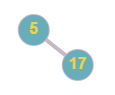
Level order traversal is [ 17, 5 ] and [ 5, -1, 17 ], if you return any of this tree you will get the output as 1.
Hint
Hint 1
Hint 2
Think recursively by dividing the array into two half.
Approaches (2)
Approach 1
Approach 2
Recursive Approach
As the given array is sorted and we want a balanced tree such that every node has a right subtree with a greater value and a left subtree with a smaller value. We can think of making the middle element of the array root node, this will ensure that both left and right subtree have equal elements thus maintaining the balance of the tree. All elements left of middle elements are smaller and go into the left subtree of the root node. Elements on the right of middle elements are greater thus goes on the right subtree. And also for making the left subtree a ‘balanced BST’ we can further divide it into two halves, same for the right subtree. Recursively following the procedure overall nodes will result in a balanced binary search tree.
Algorithm :
- Let’s say we need to find a balanced BST for ‘ARR[1:N]’, where ‘N’ is the size of array ‘ARR’.
- Base case - if ‘N == 1’ i.e. only one element is present, then make it a root node.
- Else, Declare a variable say ‘mid’ that stores the middle index of the array.
- The ‘ARR[mid]’ forms the root node of balanced BST
- For left subtree recursively call the function with the left part of array i.e ‘ARR[1: mid-1]’
- For the right subtree recursively call the function with the right part of the array i.e. ‘ARR[mid+1:N]’
- Add returned left subtree and right subtree to the left and right child, respectively of the root node.
- Return root node.
Time Complexity
O(N), where ‘N’ is the size of the given array.
The recurrence relation for the above solution is T(N) = 2 * T(N / 2) + C , where ‘C’ is constant time. Solving this using substitution method gives us the overall complexity of O(N).
Space Complexity
O(log(N)), where ‘N’ is the size of the given array.
The recursion call stack will store function calls up to the height of the tree, and the tree is balanced thus height in the worst case will be log(N).
Hence the overall space complexity will be O(log(N))
Video Solution
Unlock at level 3
(75% EXP penalty)
Code Solution
(100% EXP penalty)
Convert Sorted Array to BST
C++ (g++ 5.4)
Console



