Convex polygon

Hard
0/120
Average time to solve is 15m
profile
Contributed by
4 upvotes
Asked in company
alibaba

Problem statement

You are given an array ‘POINTS’ of size ‘N’. Each element of ‘POINTS’ contains two integers, ‘[X, Y]’ representing a point on the cartesian plane. These points, when joined sequentially, form a polygon. The task is to find if this polygon is convex (Convex polygon).

Example: 
‘POINTS’ = [ [0, 0], [5, 0], [5, 5], [0, 5] ], ‘N’ = 4.

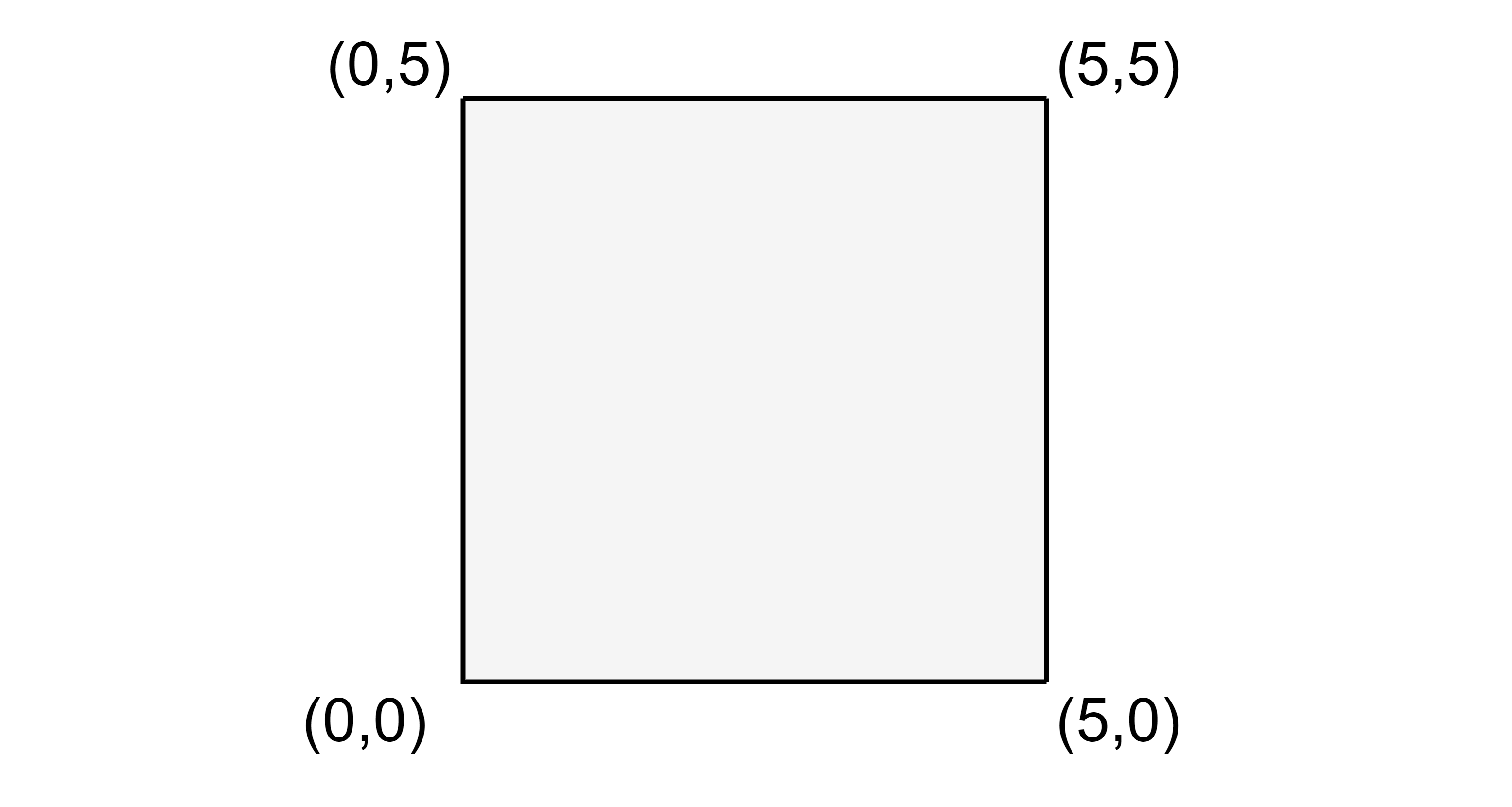
example

As the given polygon is a convex polygon, you should return ‘True’ as the answer.
Note: 
1. The polygon formed by the given points is always a Simple polygon, i.e., exactly two edges intersect at each vertex, and the edges otherwise don’t intersect each other.

2. All the given points are unique.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer ‘T’ which denotes the number of test cases. Then, the ‘T’ test cases follow.

The first line of each test case contains an integer ‘N’ denoting the size of the array ‘POINTS’. Then, ‘N’ lines follow.

Each line contains two integers, ‘X’ and ‘Y’, representing an element in the array ‘POINTS’.
Output format: 
For every test case, if the given polygon is convex, return ‘True’. Otherwise, return ‘False’.
Note: 
You do not need to print anything; it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 100
1 <= N <= 1000
-10^4 <= Value in each element of ‘POINTS’ <= 10^4

Time limit: 1 second

Sample input 1:

2
6
0 0
10 0
7 5
10 10
0 10
2 5
5
-10 5
-10 10
-5 15
0 15
0 5

Sample output 1:

False
True

Explanation of sample input 1:

Test Case 1:

sample1

The interior angle at the vertex ‘(2, 5)’ is more than 180 degrees, so the given polygon is not convex. Thus, you should return ‘False’ as the answer.

Test Case 2:

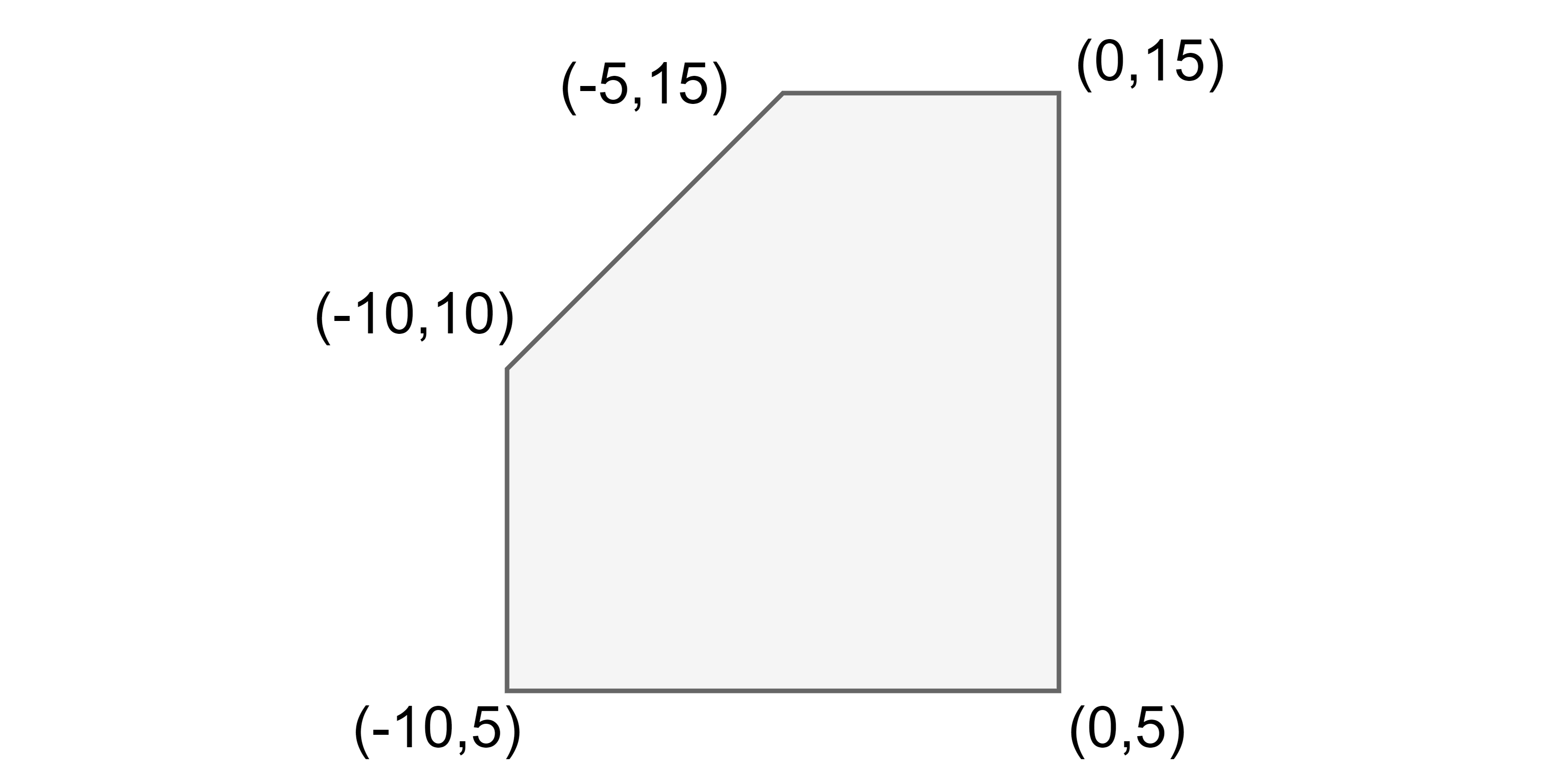
sample2

As the given polygon is a convex polygon, you should return ‘True’ as the answer.

Sample input 2:

2
5
0 0
5 0
5 5
2 8
0 5
5
5 0
15 0
15 10
5 10
10 5

Sample output 2:

True
False
Hint

For any edge, what should be the positions of every vertex w.r.t. it?

Approaches (2)
All vertices should be at one side of each edge

For any edge ‘E’ in a convex polygon, every vertex ‘V’ should be either at one side of it (above/below) or on it. Consider the following two examples:

 

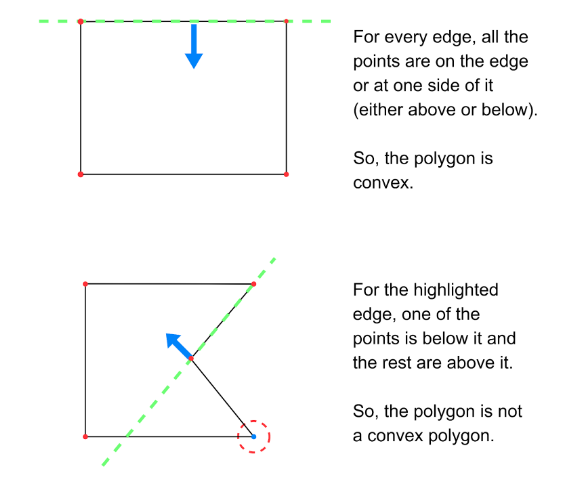
Let ‘AB’ be the edge between the vertices ‘(A, B)’ and ‘C’ be any vertex.

 

‘POS = (B.x - A.x) * (C.y - A.y) - (B.y - A.y) * (C.x - A.x)’ (Position of point ‘C’ w.r.t. ‘AB’).

 

Here, ‘POS’ is the Z-component of the cross-product between the vectors ‘AB’ and ‘AC’. To decide if ‘C’ is below or above ‘AB’:

  • Suppose the angle between ‘AB’ and ‘AC’ is ‘T’ (‘0 < T < 180’), then the Z-component of ‘AB x AC’ will be coming out of the page. Thus, we have a positive ‘POS’ value.
  • Suppose the angle between ‘AB’ and ‘AC’ is ‘-T’ (‘0 < T < 180’), then the Z-component of ‘AB x AC’ will be going into the page. Thus, we have a negative ‘POS’ value.

 

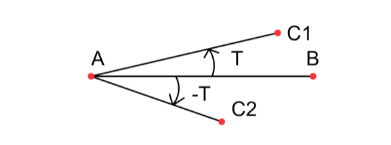
In other words, ‘POS’ can be:

  • Positive: If ‘C’ is on one side of the edge ‘AB’ (let’s say above).
  • Negative: If ‘C’ is on the other side of the edge ‘AB’ (let’s say below).
  • Zero: If ‘C’ is on edge ‘AB’.

So, for any edge, if we find two vertices having opposite signs of ‘POS’, then we declare that the polygon is not convex.

 

Algorithm:

  • Run a loop where ‘a’ ranges from ‘0’ to ‘N - 1’ to iterate through all the edges ‘ab’ and ‘bc’:
    • Set ‘POSITIVE = 0’. To count the number of positive 'POS' values.
    • Set ‘NEGATIVE = 0’. To count the number of negative 'POS' values.
    • Set ‘b = (a + 1) % N’. To handle the boundary case when ‘a = N - 1’.
    • ‘xA = POINTS[a][0]’ and ‘yA = POINTS[a][1]’. Coordinates of point ‘a’.
    • ‘xB = POINTS[b][0]’ and ‘yB = POINTS[b][1]’. Coordinates of point ‘b’.
    • Run a loop where ‘c’ ranges from ‘0’ to ‘N - 1’ to iterate through all the vertices:
      • ‘xC = POINTS[c][0]’ and ‘yC = POINTS[c][1]. Coordinates of point ‘c’.
      • ‘POS = (xB - xA) * (yC - yA) - (yB - yA) * (xC - xA)’.
      • If ‘POS > 0’, then:
        • ‘POSITIVE += 1’.
      • Else, if ‘POS < 0’, then:
        • ‘NEGATIVE += 1’.
    • If ‘POSITIVE > 0’ and ‘NEGATIVE > 0’, then we have vertices on both sides of the edge ‘ab’:
      • Return ‘False’ as the polygon is not convex.
  • Return ‘True’ as the answer.
Time Complexity

O(N^2), where ‘N’ is the size of the array ‘POINTS’.

 

There are ‘N’ edges, and for each edge, we iterate through all the ‘N’ vertices. Thus, the time complexity is ‘O(N^2)’.

Space Complexity

O(1).

 

Since we are not using any extra space, space complexity is constant.

Code Solution
(100% EXP penalty)
Convex polygon
Full screen
Console