Problem
Submissions
Hints & solutions
Discuss
Count Nodes within K-distance
Hard
0/120
Average time to solve is 10m
Problem statement
You are given a connected, undirected and acyclic graph with some of the nodes as marked and a positive number 'K'. You need to return the count of all such nodes which have a distance from all marked nodes less than 'K', which means every node whose distance from all marked nodes is less than 'K', should be counted in the result.
A graph is said to be connected if there is a path between every pair of vertex, i.e., from every vertex to any other vertex, there should be some path to traverse and acyclic means that the graph does not contain cycle and undirected means that the edge is bidirectional and one can move in both directions.
Example:
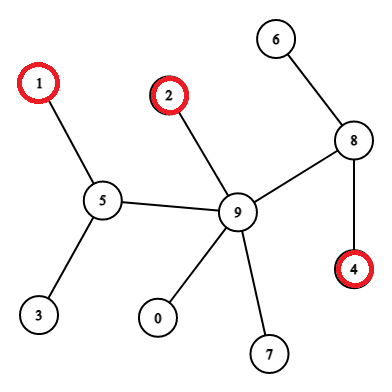
Marked Nodes are Circled with red colour.
Now consider this example of the graph. Here nodes 1,2, and 4 are marked, and let us take the value of K as 3, i.e., we have to find all the nodes at a distance less than 3 from all the marked nodes. We can see that nodes with index 5,9,8,2,0,7 have distances less than 3 from all marked nodes; therefore, the total count of nodes will be 6.
Detailed explanation ( Input/output format, Notes, Images )
Input format :
The first line contains two space-separated integers 'V' and 'E', denoting the number of vertices and edges in the graph.
The next 'E' lines contain two space-separated integers denoting the vertices between whom edges exist.
The next line contains a single integer 'K' denoting the distance.
The next line contains a single integer 'M' representing the number of marked nodes in the graph.
The next line contains 'M' space-separated integers representing marked nodes.
For each test case, print an integer denoting the count of the nodes which are less than 'K' distance from all the marked nodes.
The output of every test case will be printed in a separate line.
You don’t have to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= 'V' <= 10^4
0 <= 'E' <= 10^4
1 <= |'V'| <= 'V'
1 <= 'K' <= 35000
1 <= 'M' <= 7000
Time Limit: 1 sec.
Sample Input 1 :
10 9
2 1
1 4
1 9
3 4
4 6
4 7
4 8
5 6
6 10
3
3
1 2 4
Sample Output 1 :
8
Explanation of the sample input 1:

From the test case, we can draw the following graph, and it is given that 1,2 and 4 are marked, and the value for K is 3, so in the above graph, we can see that node with index 1, 2, 3, 4, 5,6, 7, 8 have distances less than 3 from all the marked nodes also shown in the figure so the answer will be 8.
Sample Input 2 :
10 9
2 1
1 4
1 9
3 4
4 6
4 7
4 8
5 6
6 10
3
3
1 4 8
Sample Output 2 :
10
Explanation of the sample input 2:
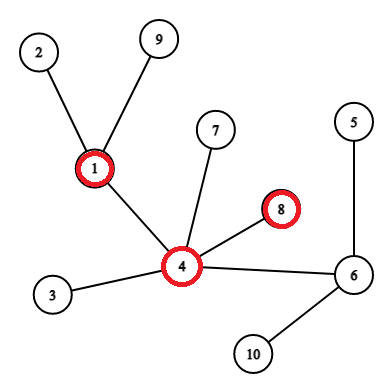
From the test case, we can draw the following graph, and it is given that 1,4 and 8 are marked, and the value for K is 3, so in the above graph, we can see that all the nodes are at 3 or less than 3 from all the marked nodes so the answer for this case will be a total number of nodes that is 10.
Hint
Hint 1
Try and think of how you can check for each node, whether its distance is less than the K or not from marked nodes.
Approaches (1)
Approach 1
Using BFS
Approach:
In this approach, we will be using the bfs traversal of the graph. Finding the maximum distance between any two marked nodes considering all pairs of marked nodes one by one. After calculating the maximum distance, we will be checking each node's distance from both of these nodes( which are farthest from each other). If the distance of the node is less than K from both nodes, that means it will be at a distance less than K from all the marked nodes because these two nodes represent the extreme limit of all marked nodes, i.e., if a node lies in the limit, then it will be at a distance less than K from all marked nodes otherwise not. Now by doing a bfs traversal on the graph starting from any node, we can find the first extreme of both nodes. Now by again doing bfs from this node, we can find the second extreme node to avoid one extra bfs traversal for finding nodes distance from the first extreme; we can find these distances in the same bfs we are doing to find the second node. For finding distances of the node from the second extreme node, we will need one more bfs traversal. After getting all distances, we can check whether the distances are less than K for the count.
Steps:
- Create a function called BFSUTIL, which we will use to traverse the graph and store the distance of nodes from extreme and will return the most extreme marked node from node U.this function will take parameters array storing edges, a boolean array for marked nodes, node U and array for storing distances. BFSUTIL(GRAPH,MARK,U,DISTANCES)
- Declare a variable for storing the previous marked node ‘PREMARKED.’
- Initialize a queue for bfs traversal ‘Q’ and push node U in the queue and initialize its distance as 0, i.e., DISTANCES.get(U)=0;
- Now run a loop until all the nodes are processed or the queue is empty.
- Now do Q.POLL() and check if it is marked in the boolean array and if it is already marked change last marked as the current node.
- Now loop over all neighbors of U and update their distance before pushing in the queue, i.e., if DISTANCES.GET(V) is -1 update it.
- Finally, return the PREMARKED node.
- Now for the main function, which returns the count of nodes, prepare the graph and the marked nodes.
- Declare three arrays TEMP, DISTANCEFROMFIRSTEXTREME, DISTFROMSECONDEXTREME, to find the first distant node and to store distances from both extremes, respectively.
- Run three bfs traversals as said in approach.
- Finally, check for the distances which are less than K and add it to the final COUNT, which was initialized as ZERO initially.
- Return COUNT.
Time Complexity
O(V+E), Where ‘V’ denotes the number of vertices in the graph, and ‘E’ denotes the number of edges in the graph.
Since we are doing a bfs traversal, which is taking O(V+E) time complexity.
Space Complexity
O(V), Where ‘V’ denotes the number of vertices in the graph.
As we are using Arraylist to store vertices.
Code Solution
(100% EXP penalty)
Count Nodes within K-distance
Javascript (node v10.20.0)
Console



