Count Special Nodes In Generic Tree

The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow. The first and only line of each test case or query contains Elements in level order form separated by space (as per done in class). Order is - Root_data, n (No_Of_Child_Of_Root), n children, and so on for every element Elements are in the level order form and on a level from left to right. For example, the input for the tree depicted in the below image would be :

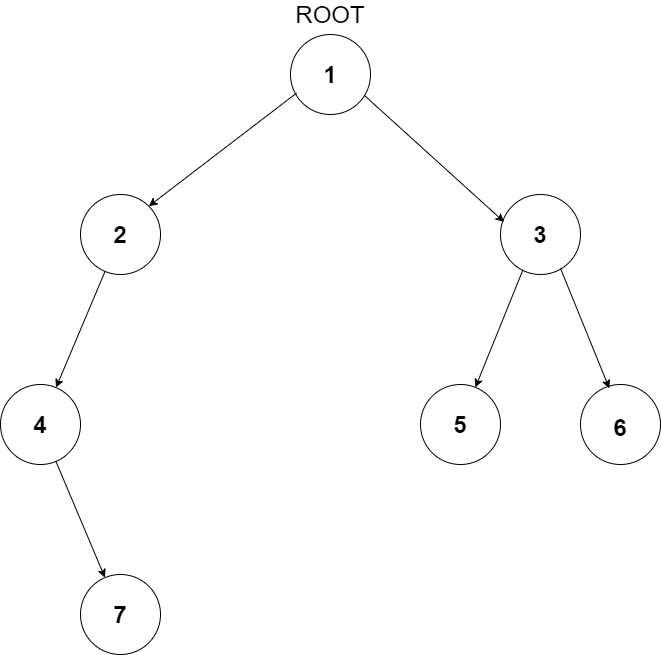
1 2 2 3 1 4 2 5 6 1 7 0 0 0 Explanation : Level 1 : The root node of the tree has value 1 hence the first value. Now, on the second line, we have 2 which means root has 2 children. The values of the two children are 2 and 3 which is given on the third line. Level 2 : Now, in the level order traversal, we visit the data node 2 and see the number of children it has, which is given on the fourth line followed by the value(s) of its child/children. Here, data node 2 has only 1 child and hence the value mentioned on the fifth line is 4. Next node in the level order traversal is the data node 3. It has 2 children as given on the 6th line. After that, on the 7th line, we have the values of its children which are 5 and 6. Level 3 : The first node on level three is 4 and it has 1 child as mentioned on the eighth line. On the ninth line, we have the value of the child as 7. The second node is 5 which has 0 or no children and has been mentioned on the tenth line. The third node is 6 which has 0 or no children and has been mentioned on the eleventh line. Level 4 : There is only 1 node at level 4 which is 7 and has 0 children or no children as mentioned on the twelfth line. As every node has 0 children now the input ends.

The above format was just to provide clarity on how the input is formed for a given tree. The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as: 1 2 2 3 1 4 2 5 6 1 7 0 0 0

For Test Case 1: We have 4 Special Nodes: 10 Path: 10 20 Path: 10 -> 20 30 Path: 10 -> 30 50 Path: 10 -> 20 -> 50 For Test Case 2: We have 3 Special Nodes: 5 Path: 5 4 Path: 5 -> 4 1 Path: 5 -> 4 -> 1

DFS

We will do a recursive Depth First Search keeping a vector/list to check for the distinct element.

We start the recursive DFS from the “root” node with an empty vector/list.
Let’s say we are at some node “x” of the Tree with a vector/list containing all the elements from root to that node.
If the value of the node “x” is present in the vector/list then it means our distinct element condition is violating so return 0.
Else insert the value of node “x” in vector/list and initialize the count of special nodes with 1.
Now recurse for children of node “x” with updated vector/list to count the special nodes in subtree of “x”.
Now delete the value of node “x” from vector/list to make sure that all other child elements have been removed from the vector/list when we move to the next child
Return the total count of special nodes

Time Complexity

O(N*N), where N is the number of nodes in Generic Tree.

As we are visiting each node of the tree once and checking if the value of the node already exists or not then pushing the value of nodes in vector/list, which is O(N) on average. So Overall Time Complexity is O(N*N).

Space Complexity

O(N), where N is the number of nodes in Generic Tree.

As we are doing recursive DFS which can at max have a depth of O(N) and also our vector/list can have max size N.

Count Special Nodes In Generic Tree

Problem statement

Sample Input 1 :

Sample Output 1 :

Explanation to Sample Input 1 :