Cycle Detection In Undirected Graph

Moderate
0/80
profile
Contributed by
240 upvotes
Asked in companies
AmazonAdobeSamsung

Problem statement

You have been given an undirected graph with 'N' vertices and 'M' edges. The vertices are labelled from 1 to 'N'.

Your task is to find if the graph contains a cycle or not.

A path that starts from a given vertex and ends at the same vertex traversing the edges only once is called a cycle.

Example :

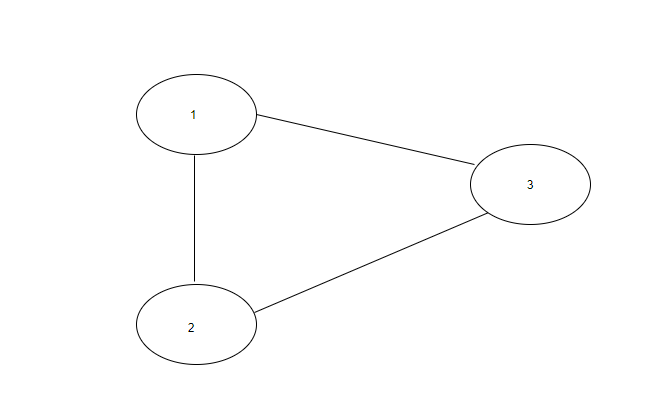
In the below graph, there exists a cycle between vertex 1, 2 and 3.

Example

Note:

1. There are no parallel edges between two vertices.

2. There are no self-loops(an edge connecting the vertex to itself) in the graph.

3. The graph can be disconnected.

For Example :

Input: N = 3 , Edges =  [[1, 2], [2, 3], [1, 3]].
Output: Yes

Explanation : There are a total of 3 vertices in the graph. There is an edge between vertex 1 and 2, vertex 2 and 3 and vertex 1 and 3. So, there exists a cycle in the graph.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains two single space-separated integers ‘N’ and ‘M’ representing the total number of vertices and edges, respectively.

The next ‘M’ lines contain two single space-separated integers representing an edge of the graph.
Output Format: 
For each test case, the only line of output will return “Yes” if there exists a cycle in the graph. Else print “No”.
Note: 
You are not required to print the expected output, it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 10
1 <= N <= 5000
0 <= M <= min(5000, (N * (N - 1)) / 2)
1 <= edges[i][0] <= N 
1 <= edges[i][1] <= N 

Time Limit: 1 sec
Sample Input 1:
1
3 2
1 2
2 3
Sample output 1:
No
Explanation of Sample output 1:
 The above graph can be represented as

Example

There are a total of 3 vertices in the graph.There is an edge between vertex 1 and 2 and vertex 2 and 3. So, there is no cycle present in the graph.
Sample Input 2:
2
4 0 
4 3
1 4
4 3
3 1
Sample output 2:
No
Yes
Hint

Try to use DFS to solve the problem.

Approaches (3)
DFS Approach (Slow)

There is a cycle in the graph only if there is a back edge (back edge is an edge that connects a vertex to another vertex that is discovered before it's parent) present in the graph. To detect a back edge, we will keep track of vertices that have been already visited. If we reach a vertex that is already visited and is not the parent vertex of the current vertex, then there is a cycle in the graph. 

 

Here is the complete algorithm:

  1. We create a graph using the ‘EDGES’ array and initialise an array ‘VISITED’ to keep track of the visited vertices.
  2. We iterate over all vertices of the graph and if the vertex is unvisited, we call the ‘IS_CYCLE’ function from that vertex. The ‘IS_CYCLE’ function works as follows:
    1. Mark the current vertex true in the ‘VISITED’ array.
    2. Find all the adjacent vertices of the current vertex.
      1. If an adjacent vertex is not visited
        1. Recursively call the ‘IS_CYCLE’ function for the adjacent vertex.
        2. If the recursive function returns true, then return true.
      2. Else if the adjacent vertex is already visited and is not the parent vertex of the current vertex.
        1. Return true.
    3. Finally, return false.
  3. If the ‘IS_CYLCE’ function returns true, then return “Yes”. Else return “No”.
Time Complexity

O(N + M), where ‘N’ is the number of vertices and ‘M’ is the number of edges in the graph.

 

In the worst case, we are visiting each vertex and edge of the graph only once. Hence, the time complexity is O(N + M).

Space Complexity

O(N), where ‘N’ is the number of vertices in the graph.

 

We are using an extra array ‘VISITED’ to keep track of visited vertices and in the worst case, we have all the vertices of the graph in the recursion stack. Hence, the space complexity is O(N). 

Code Solution
(100% EXP penalty)
Cycle Detection In Undirected Graph
Full screen
Console