Decode Ways

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
16 upvotes
Asked in companies
UberAdobeLinkedIn

Problem statement

Given a string ‘strNum’ which represents a number, your task is to find the ways to decode the given string ‘strNum’.

The format of encoding is as follows: ‘A’ - 1, ‘B’ - 2, ‘C’ - 3, ‘D’ - 4, ……………, ‘Z’ - 26.

Encoding is possible in letters from ‘A’ to ‘Z’. There is an encoding between character and number.

Example :

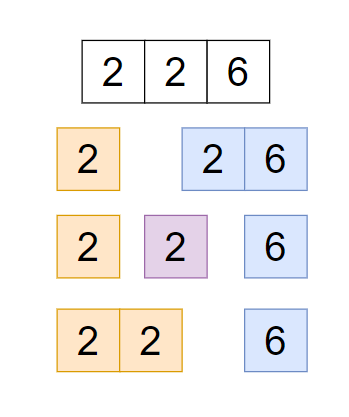
subsequence

‘n = 226’ so we can decode ‘226’ in such a way-

‘BZ = 2-26’, as B maps to 2 and Z maps to 26.

‘BBF = 2-2-6’

‘VF = 22-6’

‘226; can be decoded in three ‘BZ’, ‘BBF’, ‘VF’ possible ways.

Point to be noticed we can’t decode ‘226’ as ‘226’ because we have no character which can directly map with ‘226’ we can only decode numbers from ‘1’ to ‘26’ only.

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first line of input contains an integer ‘T’ denoting the number of test cases. The 'T' test cases follow.

The first line of each test case contains a single string ‘strNum’.

Output Format :

For each test case, print an integer denoting the ways of decodes.

Note :

1. You do not need to print anything, it has already been taken care of. Just implement the given function.
2. Ways of decodes can be very high, so return answer modulo 10^9+7.

Constraints :

1 <= T <= 50
1 <= N <= 10^4

Time limit: 1 second

Sample Input 1 :

2
143
10

Sample Output 1 :

2
1
Explanation of sample input 1 :
Test Case 1:

‘strNum = 143’ so we can decode ‘143’ in such a way-

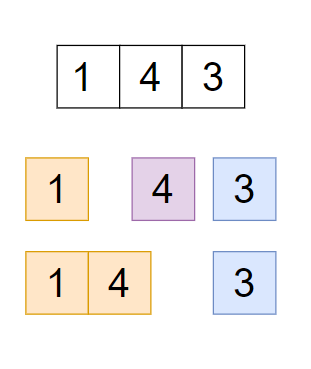
subsequence

There are only ‘2’ ways to decode the number ‘143’ is
‘ADC = 1-4-3’, as A maps to 1, D maps to 4 and C maps to 3. 
‘NC= 14-3’, as N maps to 14 and C maps to 3. 

Hence return ‘2’,
There can possibly be another partition ‘1-43’, but we can’t map ‘43’ with any character of ‘1’ to ‘26’ so it is not possible.

Test Case 2:

Only one mapping of ‘10’ is possible with the character ‘J’.
So return ‘1’.

Sample Input 2 :

2
1234
333

Sample Output 2 :

3
1
Hint

Try to find all the possible combinations.

Approaches (2)
Brute Force

The basic idea is that, try to use each and every possible combination.

 

  • Use a function ‘decodeWaysHelper(strNum,n)’, where ‘strNum’ is a given number as a string, ‘n’ is the size of ‘strNum’. And ‘decodeWaysHelper’ returns the number of decode ways.
  • If ‘n==0’ or ‘n==1’, then return ‘1’, because a single number can form only one character/ one way.
  • If ‘strNum[n-1]’ is ‘0’ then return ‘0’ because we don't have a mapping of ‘0’ with any character.
  • Else use a variable ‘count=0’ to store answer for first ‘n’ number of ‘strNum’
  • called ‘decodeWaysHelper(strNum,n-1)’, stored the result in the ‘count’ variable, because the last digit can be from ‘1’ to ‘9’.
  • If ‘strNum[n-2]==1’ then call ‘decodeWaysHelper(strNum,n-2)’ because last two digits can be from ‘11’ to ‘19’
  • If ‘strNum[n-2]==2 and strNum[n-1]<7’ then call ‘decodeWaysHelper(strNum,n-2)’ because the last two digits can be from ‘20’ to ‘26’.
  • At the end return count.
Time Complexity

O(2^N). Where ‘N’ is the size of a given ‘strNum’ as a string.

 

We are using a ‘2 choose’ recursion of size ‘N’. ‘2 choose’ recursion means at every point of the stage we have two possibilities to proceed either in ‘n-1’ or ‘n-2’ as shown in the above approaches.

Space Complexity

O(N). Where ‘N’ is the size of a given ‘strNum’ as a string.

 

We are using an ‘N’ size of the call stack in recursion.

Code Solution
(100% EXP penalty)
Decode Ways
Full screen
Console