Problem
Submissions
Hints & solutions
Discuss
Defend The Village
Moderate
0/80
Average time to solve is 20m
Problem statement
You are given an array/list of positive integers ‘HOUSES’ that represents the positions of 'N' different houses in Ninja’s village on a horizontal line. There is an attack by the enemy that a group of 'M' Ninjas positioned at different houses can stop as long as the houses are within their radius range. The positions of these 'M' Ninjas are given in an array/list 'NINJAS'.
Your task is to return the minimum radius standard of the defender Ninjas so that those Ninjas could defend all houses in 'HOUSES' array.
Example :
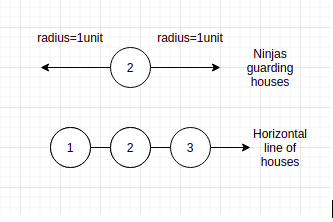
Suppose given ‘HOUSES’ is [1,2,3] and ‘NINJAS’ is [2] then
The defending radius range of the ninjas (‘NINJAS’) is 1 since there is only one ninja that is defending at position 2, and if we use the radius 1 standard, then all the houses can be protected.
Detailed explanation ( Input/output format, Notes, Images )
Input Format :
The first line of input contains a single integer ‘T’ denoting the number of test cases given. Then next ‘T’ lines follow:
The first line of each test case input contains two space-separated integers, where the first integer 'N' represents the length of the ‘HOUSES’ array while the second integer 'M' represents the length of ‘NINJAS' array.
The second line of each test contains ‘N’ space-separated integers which are the elements of the position of houses (‘HOUSES’) array.
The third line of each test contains ‘M’ space-separated integers which are the elements of the position of Ninjas (‘NINJAS’) array.
Output Format :
For every test case, print an integer denoting the minimum radius standard of (‘NINJAS’) Ninjas so that those Ninjas could defend all houses.
Note :
1. You do not need to print anything, it has already been taken care of. Just Implement the given function.
2. Notice that all the ninjas (‘NINJAS’) follow your radius standard, and the defending radius will be the same.
Constraint :
1 <= T <= 10
1 <= N, M <= 3 * 10^3
1 <= HOUSES[i], NINJAS[i] <= 10^9
Where 'HOUSES[i]' represent the position of 'ith' house and 'NINJAS[i]' represent the position of 'ith' Ninja.
Time Limit: 1 sec
Sample Input 1 :
2
4 2
1 2 3 4
1 4
2 1
1 5
2
Sample Output 1 :
1
3
Explanation For Sample Output 1 :
Test Case 1:
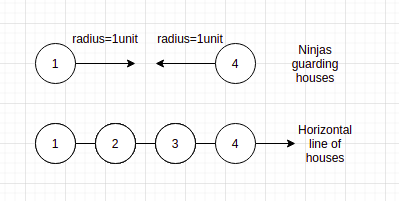
1 is the required standard radius range that the Ninjas should have to defend/cover to protect all the houses
Since the given positions of the houses are 1, 2, 3 and 4 and the given positions of the two Ninjas who would be available to defend all the houses are at house 1 and house 2. So if the minimum radius range standard is kept as 1 then they would be able to successfully defend the houses in their village and defeat the enemies.
Test Case 2:
3 is the required standard radius range that the Ninjas should have to defend/cover to protect all the houses.
Since the given positions of the houses are 1 and 5 and the given position of the only Ninja who would be available to defend all the houses is at house 2. So if the minimum radius range standard is kept as 3 then the Ninja would be able to successfully defend the houses in the village and defeat all the enemies.
Sample Input 2 :
2
4 4
1 9 17 25
3 7 15 20
3 1
1 2 3
2
Sample output 2 :
5
1
Hint
Hint 1
Hint 2
Try to use a brute-force approach to iterate over the ‘HOUSES’ and ‘NINJAS’ arrays/list and find the minimum required standard radius range.
Approaches (2)
Approach 1
Approach 2
Brute Force
A possible solution could be to take each house ‘i’ (‘HOUSE’[i]) and check if it has a Ninja guarding it that is if (‘HOUSE’[i] == ‘NINJA’[i]) both have the same position. Then this house ‘i’ is already equipped with a Ninja and we can continue to evaluate the next house.
If the position of house ‘i' is smaller than all elements of the ‘NINJAS’ array, record the distance from ‘i’ to the first element of the ‘NINJAS’ array.
If the position of house ‘i’ is larger than all elements of the ‘NINJAS’ array, record the distance from ‘i’ to the last element of the ‘NINJAS’ array.
If the position of house ‘i’ in between the two adjacent elements (positions) of the ‘NINJAS’ array, calculate the distances from the left and right of ‘HOUSE’[i] respectively and take the minimum value, and only when the defending radius satisfies this value, the house ‘i’ can be covered by the defending range of the left or right Ninja. Finally, return the resultant standard radius range which can now be set for all the houses.
The algorithm to calculate the required will be:-
- Sort the ‘HOUSES’ and ‘NINJAS’ arrays in ascending order.
- Initialize a variable ‘RESULT’ for storing the maximum guarding distance of a ninja’s from a house and another variable ‘DISTANCE’ for keeping track of the possible distance calculated in every iteration.
- Now, traverse the given array of houses by iterating from 0 to ‘N’ which is the total size of the ‘HOUSES’ array.
- For every ‘HOUSE’[i], initialise a variable ‘j’ = 0 and iterate over the ‘NINJAS’ array in a while loop until we find the position of the first Ninja that is greater than or equal to the position of ‘HOUSE’[i]. Break if ‘j’ reaches the last index of the ‘NINJAS’ array or position of ‘NINJA’[i] is not less than that of ‘HOUSE’[i].
- After the while loop, for every value of ‘j’ we get we calculate the distances of the ‘HOUSE’[i] and ‘NINJA’[j] as follows:
- ‘DISTANCE’ = ‘NINJAS’[j] - ‘HOUSES’[i], when ‘j’ == 0.
- ‘DISTANCE’ = ‘HOUSES’[i] - ‘NINJAS’[‘M’-1], when ‘j’ == ‘M’-1.
- ‘DISTANCE’ = min(‘NINJAS’[j] - ‘HOUSES’[i], ‘HOUSES’[i] - ‘NINJAS’[‘j’-1]), otherwise.
- Now we keep checking if there exists a possible minimum distance radius range that is greater than our result ‘RESULT’ and update the result ‘RESULT’ with the value of ‘DISTANCE’ if such is the case.
- Finally, return the result ‘RESULT’.
Time Complexity
O(N * M), where ‘N’ is the number of elements in the array/list ‘HOUSES’ and ‘M’ is the number of elements in the array/list ‘NINJAS’.
Since we are iterating over all the elements of the array/list ‘HOUSES’[i], trying to calculate distances for every ‘NINJAS’[j] iterating over the array/list for each ‘HOUSE’[i] hence, the complexity here grows by O(N * M).
Space Complexity
O(1).
Since, here, we are using constant space therefore space complexity is O(1).
Code Solution
(100% EXP penalty)
Defend The Village
C++ (g++ 5.4)
Console


