Diagonal Traversal

Moderate
0/80
Average time to solve is 20m
profile
Contributed by
35 upvotes
Asked in companies
MicrosoftSamsungBoston Consulting Group

Problem statement

You have been given a binary tree of integers. You have to return all the diagonal paths of the binary tree. A diagonal path is one in which all the nodes pass through -1 slope line.

A binary tree is a tree in which each parent node has at most two children.

Note:

Order of return of diagonal path’s array/vector: The rightmost diagonal path must come first, and so on.
Every parent node comes first then the child node. In other words, return the diagonal element from top to bottom.

Example

Consider the given binary tree.

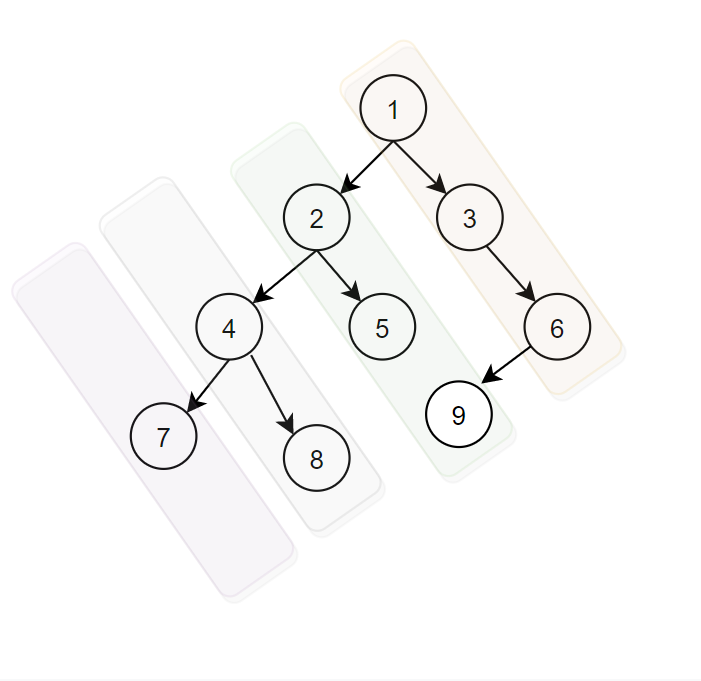
subsequence

There are 4 diagonal paths:
1 3 6
2 5 9
4 8
7
You need to return ‘1 3 6 2 5 9 4 8 7’.

Let's consider this example

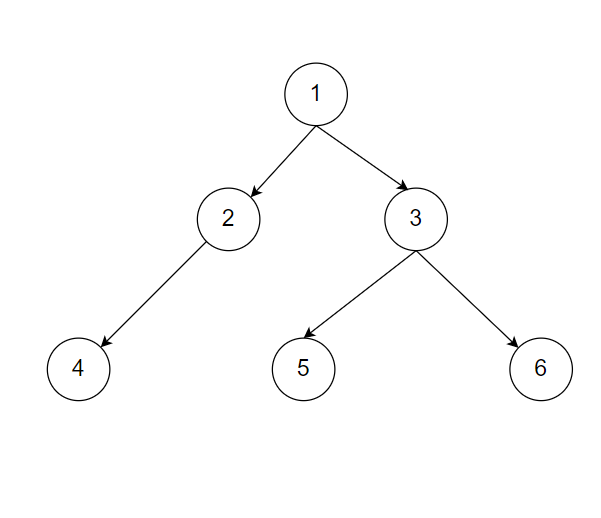
subsequence

Diagonal paths are:
1 3 6
2 5
4

You need to return ‘1 3 6 2 5 4’.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains an integer ‘T’ denoting the number of test cases.
The next ‘T’ lines represent the ‘T’ test cases.

The first line of input contains the elements of the tree in the level order form separated by a single space.
If any node does not have a left or right child, take -1 in its place. Refer to the example below.

Example:

Elements are in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

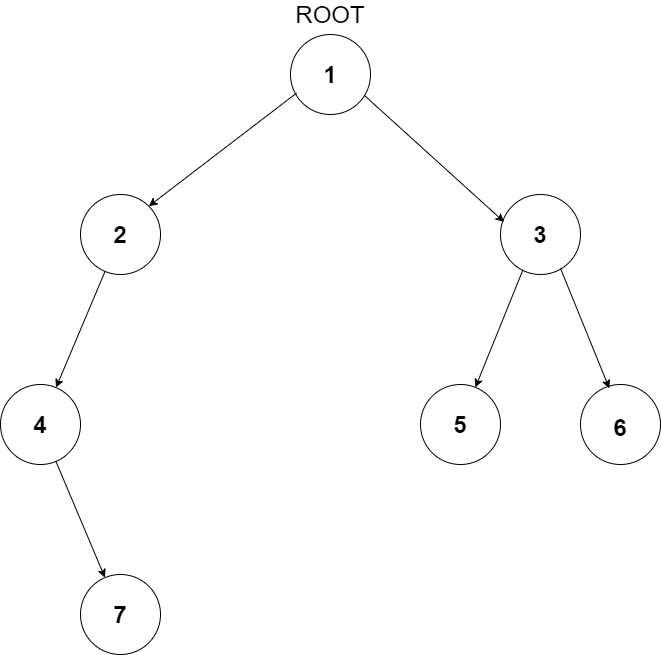
alt text

 1
 2 3
 4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (-1).
Note : 
The above format was just to provide clarity on how the input is formed for a given tree. 

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format: 
For every test case, the output prints in a single line the diagonal paths of the given binary tree.

The output of each test case will be printed in a separate line.
Note: 
You do not need to print anything; it has already been taken care of. Just return an array/list of all diagonal paths in which the rightmost diagonal path comes first, the second rightmost diagonal path comes second, and so on.
Constraint : 
1 <= T <= 10^2
1 <= N <= 3*10^3
-10^9 <= DATA <= 10^9

Where ‘N’ is the number of nodes in the tree, and 'DATA' denotes data contained in the node of a binary tree.

Time Limit: 1 sec
Sample Input 1:
2
1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1
1 2 3 -1 -1 4 5 -1 -1 -1 -1
Sample Output 1:
 1 3 7 2 5 6 4
 1 3 5 2 4
Explanation For Sample Test 1:

alt text

It is clear that '1 3 7' is the first diagonal path '2 5 6' is the second and '4' is the third diagonal path. But 5 and 6 have the same level and same diagonal path, so we need to consider a node that comes first in the pre-order traversal.
Hence the diagonal path of the above binary tree is 1 3 7 2 5 6 4.

Test case 2:

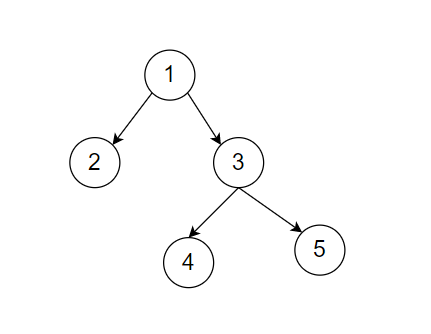
alt text

It is clear that the first diagonal path is '1 3 5', and the second is '2 4'.
Hence diagonal binary tree traversal when combined is '1 3 5 2 4'.
Sample Input 2:
2
1 -1 2 3 4 -1 -1 -1 -1
1 2 3 -1 -1 4 -1 -1 -1
Sample Output 2:
1 2 4 3
1 3 2 4
Hint

Think of a recursive approach and simultaneously using a hash map.

Approaches (1)
Recursion
  1. The idea is to use a Hash map called ‘LEVELMAP’.
  2. We use different levels and use them as keys in the map.
  3. The value of each key in the map is the vector/list of nodes.
  4. In the end, We return values from the map.
  5. Suppose the level of current node ‘CURNODE’ is ‘l’
  6. Then, the level of the right child will be ‘l’, and the level of the left child will be ‘l+1’, and ‘LEVELMAP[l] =CURNODE.DATA’
  7. And proceed the same steps for ‘LEFT’ child with level  ‘l+1’ and ‘RIGHT’ child with the level of ‘l.’
  8. Let’s consider this binary tree.

 

  1. Observe the level of binary tree
    • Level 0 => [1,3,6]
    • Level 1 => [2,5]
    • Level 2 => [4]
    • LEVELMAP = {}
    • Consider starting level for ‘1’ is 0
    • Store level in such a way that
    • LEVELMAP = { 0:[1,3,6], 1:[2,5], 2:[4] }
  2. At the end, We return value in such a form => 1 3 6 2 5 4.
Time Complexity

O(N * log(N)), Where ‘N’ is the number of nodes in a binary tree.

 

We are iterating through the binary tree once and inserting nodes into the ordered map. Iterating through the nodes will take linear time while the insert operation will take O(LogN) time. Hence overall complexity will be O(N * LogN). 

Space Complexity

O(N), Where ‘N’ is the number of nodes in a binary tree.

 

We are using a Hash map to store the nodes at a particular level. In the worst case, all the nodes could be at different levels which means for a total of ‘N’ nodes we will need an order of ‘N’ space. Also, we are using recursion and recursion stack need order ‘N’ space too. Hence the space complexity will be O(N).

Code Solution
(100% EXP penalty)
Diagonal Traversal
Full screen
Console