Numbers With Same Consecutive Differences

Moderate
0/80
Average time to solve is 20m
profile
Contributed by
3 upvotes
Asked in companies
GroMoFlipkart limited

Problem statement

You are given two integers, ‘N’ and ‘K’. The task is to return all non-negative integers having ‘N’ digits such that the absolute difference between each consecutive digit is ‘K’.

Example: 
Input: N = 2, K = 6
We need to return all two-digit numbers where the absolute difference between each consecutive digit is ‘6’. Note that ‘06’ is not a valid two-digit number. So, the answer is:
Output: [17, 28, 39, 60, 71, 82, 93]
Note: 
1. Every number in the answer should not contain leading zeroes. E.g., the number ‘09’ is invalid.

2. You can return the answer in any order.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer ‘T’ which denotes the number of test cases. Then, the ‘T’ test cases follow.

The first and only line of each test case contains two space-separated integers, ‘N’ and ‘K’, denoting the number of digits and the absolute difference between each consecutive digit.
Output format: 
For every test case, return an array of integers where each integer has ‘N’ digits, and the absolute difference between each digit is ‘K’. You may return output in any order, but the printed output will be in sorted order.
Note: 
You do not need to print anything; it has already been taken care of. Just implement the function.
Constraints: 
1 <= T <= 100
2 <= N <= 9
0 <= K <= 9

Time limit: 1 sec

Sample input 1:

2
2 0
3 6

Sample output 1:

11 22 33 44 55 66 77 88 99
171 282 393 606 717 828 939

Explanation of sample input 1:

Test Case 1:
We need to return all two-digit numbers where the absolute difference between each consecutive digit is ‘0’. So, the answer is:
Output: [11, 22, 33, 44, 55, 66, 77, 88, 99]

Test Case 2:
We need to return all three-digit numbers where the absolute difference between each consecutive digit is ‘6’. So, the answer is:
Output: [171, 282, 393, 606, 717, 828, 939]

Sample input 2:

2
4 9
2 3

Sample output 2:

9090
14 25 30 36 41 47 52 58 63 69 74 85 96
Hint

Using BFS try to create a tree where we add a new digit at each level with an absolute difference as K.

Approaches (2)
Use Breadth-first search traversal

Let’s first try to find the numbers having ‘4’ as the most significant digit (MSD). We create a tree where each node stores an integer ‘N-i’ and the least significant digit (LSD) of ‘N-i’.  Initially, the tree contains a single node, i.e., the root node with an integer ‘4’ and its LSD ‘4’. We append a new digit to the previous level until we reach 'N' levels. There are two ways to add a new digit to a child node,i.e., ‘LSD of parent node + K’ and ‘LSD of parent node - K’ (Note: For ‘K = 0’ both these values are the same, so there can only be one child). If the LSD of the new node is not between [0, 9], mark this node invalid to produce any child nodes. Following is a partial tree for ‘4’:


 



 

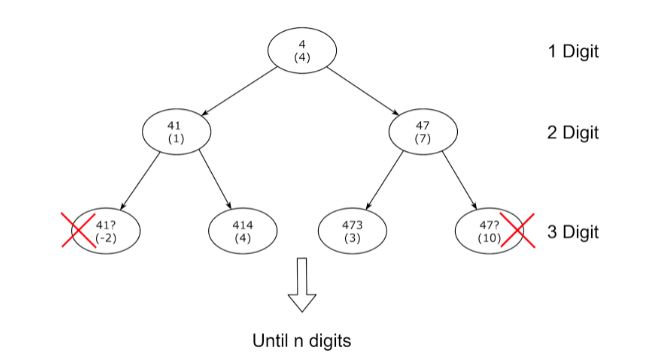
Similarly, solve for numbers having MSD as [1 to 9]. We can do a Breadth-first search (BFS) traversal of the tree to get the leaf nodes. Following are the steps for BFS:

  • Create a queue ‘BFS_QUEUE’ that stores integers. Use this queue for BFS traversal.
  • Push integers from [1 to 9] in ‘BFS_QUEUE’. These are the root nodes for trees with MSD as [1 to 9].
  • Run a loop where ‘i’ ranges from ‘2’ to 'N'. In each iteration, remove the nodes of the previous level from ‘BFS_QUEUE’ and push valid nodes of the next level:
    • ‘SIZE = SIZE_of(BFS_QUEUE)’
    • Run a loop where ‘j’ ranges from ‘1’ to ‘SIZE’:
      • ‘CUR_NUM = BFS_QUEUE.pop()’
      • ‘LSD = CUR_NUM % 10’
      • ‘CUR_NUM *= 10’
      • If ‘LSD + K’ is less than equal to ‘9’:
        • ‘BFS_QUEUE.push(CUR_NUM + LSD + K)’
      • If ‘LSD - K’ is greater than equal to ‘0’ and ‘K’ is not ‘0’:
        • ‘BFS_QUEUE.push(CUR_NUM + LSD - K)’
  • Convert ‘BFS_QUEUE’ into an array and return it as the answer.
Time Complexity

O(2^N), where ‘N’ is the number of digits.

 

In the worst-case scenario, the tree can have approximately ‘2^(N + 1)’ nodes as the tree’s height is ‘N’.

Space Complexity

O(2^N), where ‘N’ is the number of digits.

 

The queue used for BFS traversal stores the nodes at each level, and in the worst case, the last level can have approximately ‘2^N’ leaf nodes.

Code Solution
(100% EXP penalty)
Numbers With Same Consecutive Differences
Full screen
Console