Dijkstra's shortest path

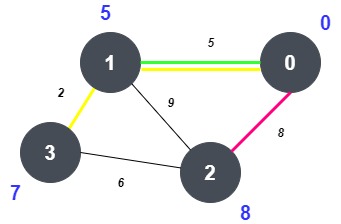
The source node is node 0. The shortest distance from node 0 to node 0 is 0. The shortest distance from node 0 to node 1 is 5. In the above figure, the green path represents this distance. The path goes from node 0->1, giving distance = 5. The shortest distance from node 0 to node 2 is 8. In the above figure, the pink path represents this distance. The path goes from node 0->2, giving distance = 8. The shortest distance from node 0 to node 3 is 7. In the above figure, the yellow path represents this distance. The path goes from node 0->1->3, giving distance = 7.

The first line contains three space-separated integers ‘V’, ‘E’ and 'S', denoting the number of vertices, the number of edges in the undirected graph and starting vertex, respectively. The next ‘E’ lines each contain three single space-separated integers ‘u’, ‘v’, and ‘distance’, denoting a node ‘u’, a node ‘v’, and the distance between nodes (u, v), respectively.

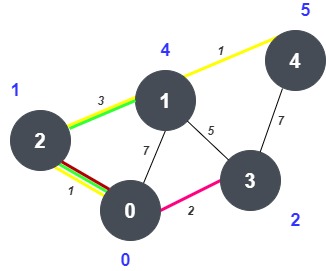
The source node is node 0. The shortest distance from node 0 to node 0 is 0. The shortest distance from node 0 to node 1 is 4. In the above figure, the green path represents this distance. The path goes from node 0->2->1, giving distance = 1+3 = 4. The shortest distance from node 0 to node 2 is 1. In the above figure, the red path represents this distance. The path goes from node 0->2, giving distance = 1 The shortest distance from node 0 to node 3 is 2. In the above figure, the pink path represents this distance. The path goes from node 0->3, giving distance = 2. The shortest distance from node 0 to node 4 is 5. In the above figure, the yellow path represents this distance. The path goes from node 0->2->1->4, giving distance = 1+3+1 = 5.

Using adjacency matrix

The idea is to maintain two arrays, one stores the visited nodes, and the other array stores the distance (element at index ‘i’ denotes the distance from node 0 to node ‘i’). We pick an unvisited minimum distance vertex, then update the distance of all its adjacent vertices considering the path from source to an adjacent vertex to pass through the picked minimum distance vertex. Repeat the process till all nodes are visited.

Steps:

We will make an adjacency matrix of size ‘V*V’, initialize all the positions to 0. Now, update the distance between two vertices in the matrix (denoted by the row number and column number) to the given distance in the input.
We also initialize the distance vector to ‘INT_MAX’ and the visited nodes vector to false. Since the distance of the source node i.e. node 0 to itself will be 0, update ‘distance[0]’ to 0.
Now, we find the shortest path for all vertices using the steps below:
1. We pick the minimum distance vertex, which is not yet visited, let’s say ‘u’. Mark it as true in the visited vector.
2. We update the distances of the adjacent vertices. Update distance[v] only if vertex ‘v’ is not already visited and the current distance of the vertex ‘v’ is greater than the distance from source vertex 0 to vertex ‘u’ plus the distance from ‘u’ to ‘v’.
3. Repeat the above steps till all the vertices are visited.
Return the distance vector, which is our required solution.

Time Complexity

O(V^2), where ‘V’ is the number of vertices in a graph.

In the worst case, using a minimum distance node, distances of ‘V’ vertices are updated. So, using ‘V’ minimum distance nodes, vertices are updated ‘V^2’ times.

Space Complexity

O(V^2), where ‘V’ is the number of vertices in a graph.

The adjacency matrix takes the size of the order ‘V^2’.

Problem statement

Sample Input 1

Sample Output 1

Explanation of sample input 1

Sample Input 2:

Sample Output 2:

Constraints: