Problem
Submissions
Hints & solutions
Discuss
Disconnect the ‘GRID’ by removing the minimum number of cities
Hard
0/120
Average time to solve is 10m
Problem statement
You are given a 2D matrix ‘GRID’ of size ‘NxM’. If there is a city in a cell ‘(i, j)’, then ‘GRID[i][j] = 1’, otherwise it’s ‘0’. A state is a maximal connected group of cities. Two cities are connected if they are horizontally or vertically adjacent to each other.
The ‘GRID’ is said to be connected if there is exactly one state. Otherwise, it’s disconnected. You are allowed to remove any number of cities from the ‘GRID’. The task is to find and return the minimum number of cities that we need to remove to disconnect the ‘GRID’.
Example :‘N’ = 3, ‘M’ = 3
‘GRID’ =
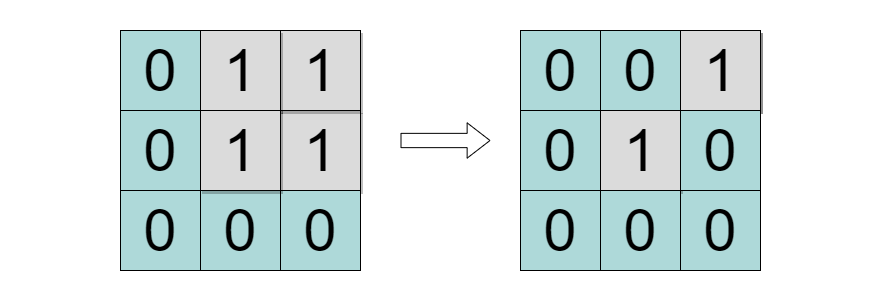
We can disconnect the ‘GRID’ by removing the cities at locations ‘(0, 1)’ and ‘(0, 2)’. Thus, you should return ‘2’ as the answer.
1. A ‘GRID’ with zero cities is also disconnected.
2. You do not need to print anything; it has already been taken care of. Just implement the function.
Detailed explanation ( Input/output format, Notes, Images )
Input format :
The first line of input contains an integer ‘T’ which denotes the number of test cases. Then, the ‘T’ test cases follow.
Each test case’s first line contains two integers, ‘N’ and ‘M’, denoting the number of rows and columns in ‘GRID’. Then, ‘N’ lines follow.
Each line contains an ‘M’ space-separated integers denoting each row’s values in ‘GRID’.
For every test case, return the minimum number of cities to remove to disconnect the island.
Constraints :
1 <= T <= 10
1 <= N, M <= 100
Value in each element of ‘GRID’ = [0, 1]
Where ‘T’ is the number of test cases, ‘N’ is the number of rows in ‘GRID’, and ‘M’ is the number of columns in ‘GRID’.
Time limit: 1 second
Sample input 1 :
2
3 4
1 0 1 1
1 1 1 1
1 0 1 1
3 4
1 1 1 1
1 0 0 1
1 1 1 1
Sample output 1 :
1
2
Explanation of sample input 1 :
Test Case 1:
We can disconnect the ‘GRID’ by removing the city at location ‘(1, 1)’.
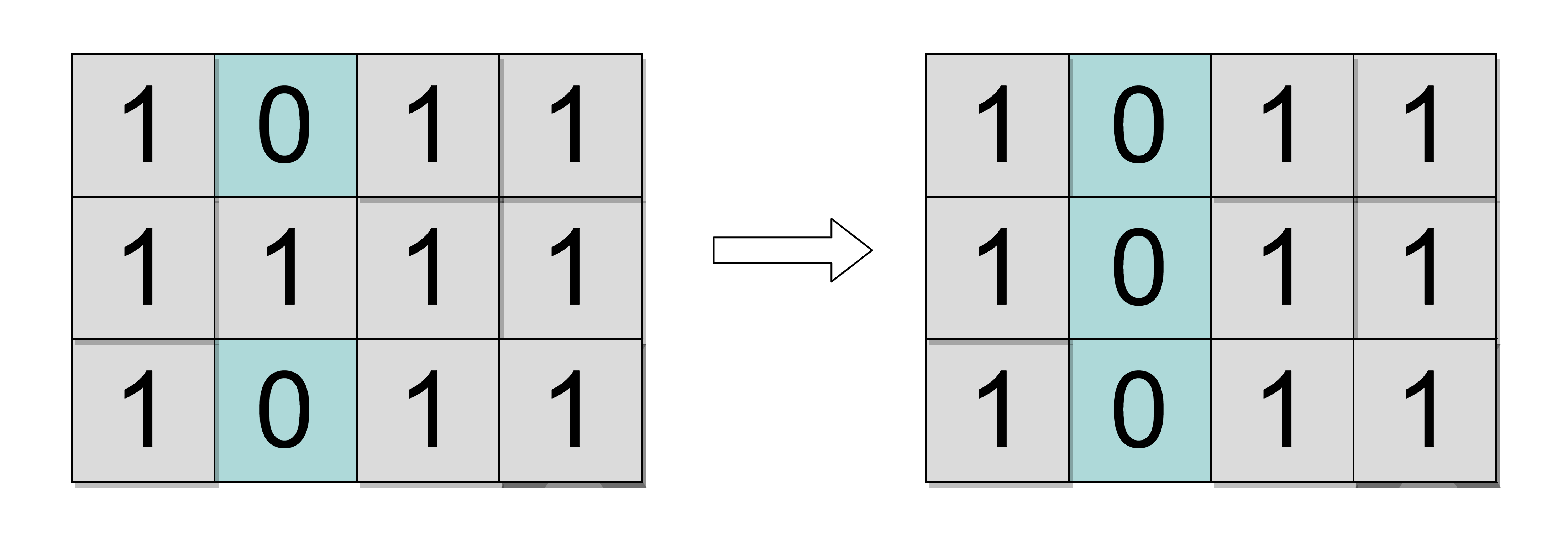
Thus, you should return ‘1’ as the answer.
Test Case 2:
We can disconnect the ‘GRID’ by removing the cities at locations ‘(1, 0)’ and ‘(1, 3)’.
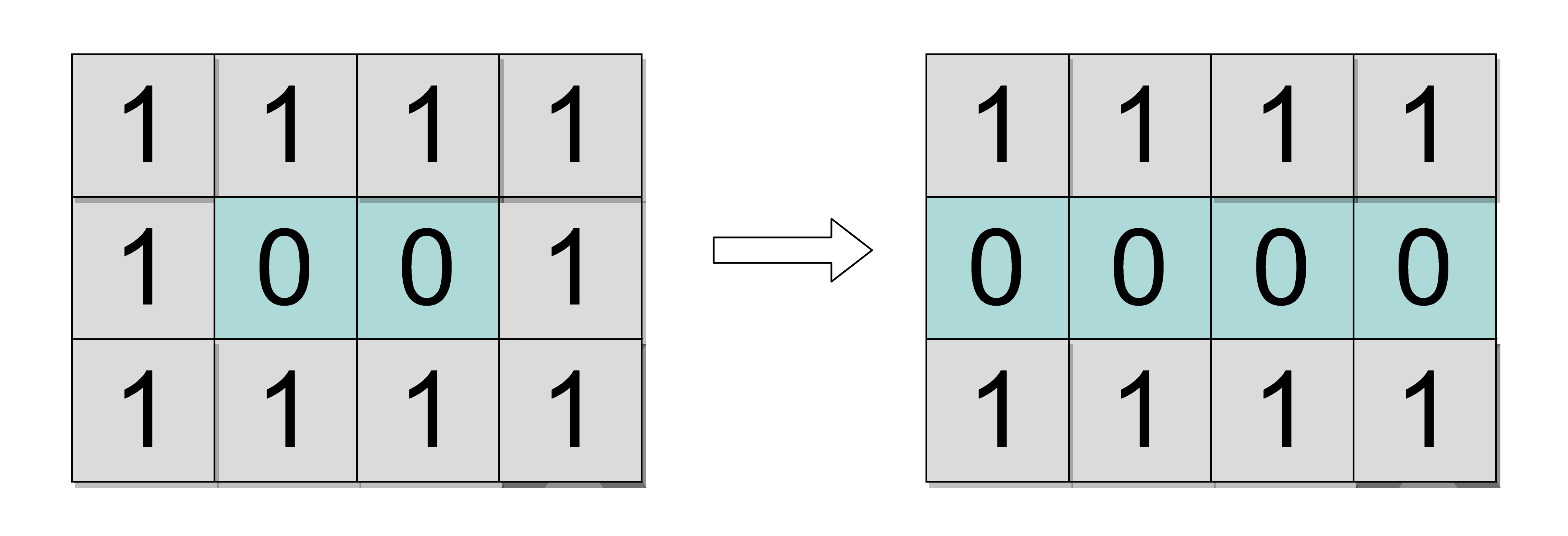
Thus, you should return ‘2’ as the answer.
Sample input 2 :
2
2 1
1
1
4 4
1 1 0 0
1 1 0 0
0 0 1 1
0 0 1 1
Sample output 2 :
2
0
Hint
Hint 1
Hint 2
If we consider the ‘GRID’ as an undirected graph, each cell’s degree is (<= 4). This shall reduce the number of possible answers in the result set drastically.
Approaches (2)
Approach 1
Approach 2
Using Depth-first search
Observation: The answer is always less than equal to two (‘<= 2’).
Proof: For any state (with ‘>= 3’ cities), every city at its boundary is connected to ‘<= 3’ cities, and between those cities, there will be at least one city connected to exactly two other cities. This city (colored red) can be of one of the following four types:
If we remove the two grey-colored cities, then the city with red color will get disconnected from its state. Now, we know that the answer will never be greater than ‘2’.
To check if the ‘GRID’ is disconnected, we can do a Depth-first search (or Breadth-first search) traversal for any arbitrary city and mark all the reachable cities from it. If some cities remain unmarked, then the ‘GRID’ is disconnected.
We try to find if the ‘GRID’ can be disconnected by removing:
- Zero cities: If the grid doesn’t contain any city or contains more than one state (already disconnected), the answer is ‘0’.
- One city: Iterate through the ‘GRID’, remove one city, and check if the ‘GRID’ becomes disconnected. If it stays connected, put the city back into the ‘GRID’ and check for the next city, and so on. If the ‘GRID’ becomes disconnected at any point during the iteration, return ‘1’ as the answer.
- Two cities: If the ‘GRID’ cannot be disconnected by removing one city, then we know that it can always be disconnected by removing ‘2’ cities. So, return ‘2’ as the answer.
The ‘isDisconnected()’ function to check if the ‘GRID’ is disconnected:
- Set ‘count = 0’. To count the number of states (connected components) in ‘GRID’.
- Initialize a 2D array ‘seen[n][m]’ and set it to ‘False’. Use it to mark visited cities.
- Run a loop where ‘i’ ranges from ‘0’ to ‘N - 1’:
- Run a loop where ‘j’ ranges from ‘0’ to ‘M - 1’:
- If ‘GRID[i][j] == 1’ and ‘seen[i][j] == False’, then we have not visited the city ‘(i, j)’:
- ‘count += 1’. Increase the number of states.
- If ‘count’ is greater than ‘1’, then ‘GRID’ is disconnected:
- Return ‘True’.
- Call ‘dfs(i, j)’ to mark the cities connected to ‘(i, j)’ as visited.
- If ‘GRID[i][j] == 1’ and ‘seen[i][j] == False’, then we have not visited the city ‘(i, j)’:
- Run a loop where ‘j’ ranges from ‘0’ to ‘M - 1’:
- If ‘count == 0’, then there are no cities in ‘GRID’:
- Return ‘True’.
- Return ‘False’ as the ‘GRID’ is connected (contains exactly one state).
The ‘dfs(integer x, integer y)’ function to mark all the cities connected to ‘(x, y)’:
- Initialize a 2D array ‘dir[4][2] = [ [0, 1], [1, 0], [0, -1], [-1, 0] ]’. Use it to move to the adjacent cell in ‘GRID’.
- Set ‘seen[x][y] = True’.
- Run a loop where ‘i’ ranges from ‘0’ to ‘3’, to move to the adjacent cities:
- Set ‘newX = x + dir[i][0]’ and ‘newY = y + dir[i][1]’. This is the location of the cell adjacent to ‘(x, y)’.
- If ‘newX >= 0’ and ‘newX < n’ and ‘newY >= 0’ and ‘newY < n’, then ‘(newX, newY)’ is a valid cell:
- If ‘GRID[newX][newY] == 1’ and ‘seen[newX][newY] == False’, then move to the new city:
- ‘dfs(newX, newY)’.
- If ‘GRID[newX][newY] == 1’ and ‘seen[newX][newY] == False’, then move to the new city:
Algorithm:
- If ‘isDisconnected() == True’, then the ‘GRID’ is already disconnected:
- Return ‘0’ as the answer.
- Run a loop where ‘i’ ranges from ‘0’ to ‘N - 1’:
- Run a loop where ‘j’ ranges from ‘0’ to ‘M - 1’:
- If ‘GRID[i][j] == 1’, then:
- Set ‘GRID[i][j] = 0’. Remove the city from ‘GRID’.
- If ‘isDisconnected() == True’, then the ‘GRID’ has become disconnected:
- Return ‘1’ as the answer.
- Set ‘GRID[i][j] = 1’. Insert the city back into the ‘GRID’.
- If ‘GRID[i][j] == 1’, then:
- Run a loop where ‘j’ ranges from ‘0’ to ‘M - 1’:
- Return ‘2’ as the answer. As the ‘GRID’ cannot be disconnected by removing one city.
Time Complexity
O((N*M)^2), where ‘N’ is the number of rows in ‘GRID’, and ‘M’ is the number of columns in ‘GRID’.
In the worst-case scenario, there are ‘O(N*M)’ cities. For each city, we check if the ‘GRID’ becomes disconnected after removing it in ‘O(N*M)’. Thus, the time complexity is ‘O((N*M)^2)’.
Space Complexity
O(N*M), where ‘N’ is the number of rows in ‘GRID’, and ‘M’ is the number of columns in ‘GRID’.
The DFS stack size will be equal to the number of cities, i.e., ‘O(N*M)’. The ‘seen’ array also needs ‘O(N*M)’ space.
Code Solution
(100% EXP penalty)
Disconnect the ‘GRID’ by removing the minimum number of cities
C++ (g++ 5.4)
Console



