Problem
Submissions
Hints & solutions
Discuss
Doctor Ninja's House
Hard
0/120
Average time to solve is 50m
Problem statement
There are ‘N’ cities and ‘M’ paths connecting them. Doctor Ninja wants to purchase a house in a city ‘X’ such that she can reach any city from the city ‘X’.
Your task is to help Ninja to find her a house ‘X’, if you are given with ‘N’ cities and ‘M’ paths.
There can be more than one house ‘X’ possible. You need to output the house ‘X’ with minimum value. If you are unable to find any such house ‘X’, then return -1.
A mother vertex in a graph G = (V, E) is a vertex v such that all other vertices in G can be reached by a path from v.
Example:
Consider the following Graph:
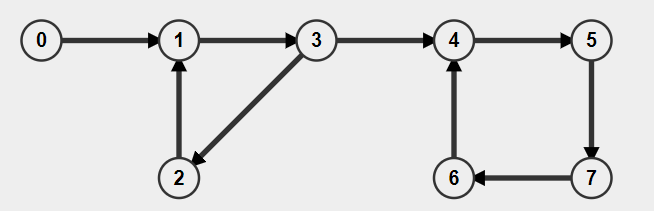
Vertices reachable from vertex 0:
0 -> 1 -> 3 -> 2 -> 4 -> 5 -> 7 -> 6
Vertices reachable from vertex 1:
1 -> 3 -> 2 -> 4 -> 5 -> 7 -> 6
Vertices reachable from vertex 2:
2 -> 1 -> 3 -> 4 -> 5 -> 7 -> 6
Vertices reachable from vertex 3:
3 -> 2 -> 1 -> 4 -> 5 -> 7 -> 6
Vertices reachable from vertex 4:
4 -> 5 -> 7 -> 6
Vertices reachable from vertex 5:
5 -> 7 -> 6 -> 4
Vertices reachable from vertex 6:
6 -> 4 -> 5 -> 7
Vertices reachable from vertex 7:
7 -> 6 -> 4 -> 5
Clearly, there is only one vertex “ 0 ” in the graph, from which all other vertices are reachable. Hence, vertex “ 0 ” is the mother vertex of the above graph.
There can be more than one mother vertices in a graph.
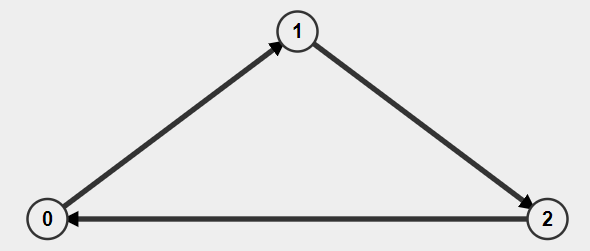
For Example, in the above graph, vertices 0, 1 and 2 are mother vertices.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains an Integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.
The first line of each test case contains two space separated integers ‘N’, denoting the number of cities (from 0 to ‘N-1’) and ‘M’, denoting the number of paths connecting cities.
Next ‘M’ lines contain two space separated integers ‘u’ and ‘v’ denoting a path from a city ‘u’ to a city ‘v’, where { u, v } ∈ N.
For each test case, return an integer ‘X’, where ‘X’ is the minimum city which Doctor can buy.
There can be more than one house ‘X’ possible. You need to output the house ‘X’ with minimum value. If you are unable to find any such house ‘X’, then return -1.
The output of each test case should be printed in a separate line.
You are not required to print anything, it has already been taken care of. Just implement the function.
Constraints :
1 <= T <= 10
1 <= N <= 10^4
1 <= M <= 10^5
0 <= X < N
Time Limit : 1 sec.
Sample Input 1:
2
4 5
0 1
2 3
0 3
2 0
1 2
5 5
0 1
3 4
2 1
3 0
2 4
Sample Output 1:
0
-1
Explanation For Sample Output 1 :
Test Case 1:
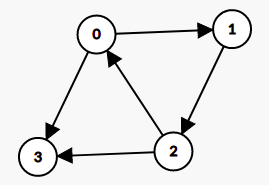
In the above graph, vertices 0, 1 and 2 are mother vertices, since we can reach every possible vertex in the graph if we start from either 0, 1 or 2. We have to output the minimum of the three vertices, hence, output should be “0”.
Test Case 2:
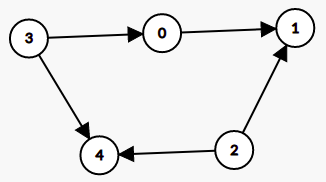
In the above graph, there is no mother vertex, since we cannot choose any such vertex from which we can reach all the vertices of the graph. Hence, output should be -1.
Sample Input 2:
2
5 5
1 0
3 4
0 2
2 1
0 3
7 7
1 3
6 0
5 6
5 2
0 1
4 1
6 4
Sample Output 2:
0
5
Hint
Hint 1
Hint 2
Think of the DFS approach. Can you think of a solution now?
Approaches (2)
Approach 1
Approach 2
Naive Approach
A trivial approach will be to perform a DFS on all the vertices and find whether we can reach all the vertices of the graph from that vertex or not.
Algorithm :
1. Implement the function 'addEdge', to store a path from vertex 'u' to vertex 'v'.
2. Implement the function 'dfs'.
1. Mark the current node as visited.
2. Recur for all the vertices adjacent to this vertex.
3. If the vertex is not visited yet, again implement the 'dfs' function for that vertex.
3. Implement the function 'findHouse'.
1. Initialize the 2-D vector 'adj' to store the adjacent vertices of a vertex.
2. Add a edge from node 'u' to node 'v' using function 'addEdge'.
3. Iterate through 0 to 'N-1' (say, iterator 'i').
1. Initialize all nodes as not visited.
2. Check for each vertex how many nodes are reachable.
3. Initialize 'flag' as zero.
4. Iterate through 0 to 'N-1' (say, iterator 'j').
1. If node is not visited, make 'flag' equal to 1 and break out of the loop.
5. If Mother vertex is found, return 1.
4. Return -1.
Time Complexity
O(N(N + M)) where ‘N’ is the number of vertices and ‘M’ is the number of edges.
The time complexity for this approach is O(N(N + M)),which is very inefficient for large graphs, because we are applying DFS on all the vertices and again applying DFS.
Space Complexity
O(‘N’), where ‘N’ is the number of vertices in a graph.
Space complexity will be O(N) due to the stack size, and in the worst case, the height of the stack can be N.
Code Solution
(100% EXP penalty)
Doctor Ninja's House
C++ (g++ 5.4)
Console


