Problem
Submissions
Hints & solutions
Discuss
Eulerian Circuit
Hard
0/120
Problem statement
You are given an edge list 'Edges' denoting a directed graph of 'N' nodes, the nodes are numbered from 0 to N - 1. Your task is to find out if the given graph is an eulerian graph or not.
A graph is an eulerian graph if it contains an Euler circuit. Euler circuit is the path in the graph that visits every edge exactly once and starts and finished at the same node.
For example:You are given the ‘Edges’ = [[0,1], [1, 2], [1, 4], [2, 3], [3, 0], [3, 1], [4, 3]], describing the following graph:

Here you can have the path, [0 -> 1 -> 2 -> 3 -> 1 -> 4 -> 3 -> 0], which is using every edge of the graph. Hence the graph is Eulerian and the answer is True.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line of input contains a single integer ‘T’ representing the number of test cases.
The first line of each test case contains two space-separated integers, ‘N’ and ‘M’, representing the number of nodes and edges in the given graph, respectively.
The following M lines of each test case contains two space-separated integers, Edges[i][0] and Edges[i][1] representing an directed edge in the graph from ‘Edges[i][0]’ to ‘Edges[i][1]’
For each test case, print ‘True’ if the given graph is eulerian, else print 'False'.
Print a separate line for each test case.
Constraints:
1 ≤ T ≤10
1 ≤ N, M ≤ 10^3
1 ≤ Edges[i][0], Edges[i][1] < N
Time Limit: 1 sec
You do not need to print anything. It has already been taken care of. Just implement the given function.
Sample Input 1:
2
5 7
0 1
1 2
1 4
2 3
3 0
3 1
4 3
2 1
0 1
Sample Output
True
False
Explanation for Sample input 1:
For the first test case, ‘edges’ = [[0,1], [1, 2], [1, 4], [2, 3], [3, 0], [3, 1], [4, 3]], describing the following graph:

Here you can have the path, [0 -> 1 -> 2 -> 3 -> 1 -> 4 -> 3 -> 0], which is using every edge of the graph. Hence the graph is Eulerian and the answer is True.
For the second test case, ‘edged’ = [[0, 1]], describing the following graph:
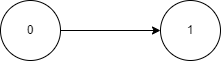
Here you can see the path [0 -> 1] uses all the edges but does not start and end at the same location. Hence there is no Euler circuit in the graph and the answer is False.
Sample Input 2:
2
3 3
0 1
1 2
2 0
4 4
1 2
2 3
3 0
0 1
Sample Output 2:
True
True
Hint
Hint 1
Find the conditions for each node for the graph to be eulerian
Approaches (1)
Approach 1
Kosaraju Algorithm
In this approach, we can see that for the graph to be Eulerian,
- All the nodes of the graph should be in the same strongly connected component
- For each node of the graph, the number of incoming and outgoing edges should be equal
If the above two conditions are met, the graph will contain an eulerian circuit and thus will be an eulerian graph.
We will use the Kosaraju algorithm to find if the graph has a single strongly connected component and then calculate the indegree and outdegree of each node.
We create a kosarajuAlorithm(adjList, n) function to get the strongly connected components of the graph, where ‘adjList’ is the adjacency list of the graph and n is the number of nodes.
Kosaraju algorithm needs a few more utility functions of the graph:
- getTranposeOfGraph(adjList) returns the transpose of the adjacency list ‘adjList.’
- topSort(adjList, stack, visited, node), which performs the topological sort on the graph and returns the order in a stack
- getStonglyConnectedComponet(adjList, currentComp, visited, node), which insert current ‘node’ in the current strongly connected component ‘currentComp’ .
Algorithm:
- In the function getTransposeOfGraph(adjList):
- Create an array of empty arrays equal to the length of adjList, called ‘transposeGraph’
- Iterate node through all the indices of adjList
- Iterate child through adjList[node] and insert node into transposeGraph[child]
- Return transposeGraph
- In the function topoSort(adjList, stack, visited, node):
- Set visited[node] to true
- iterate child through adjList[node] and if visited[child] is false
- Call topoSort(adjList, stack, visited, child)
- Insert node into stack
- In the function getStronglyConnectComps(adjList, currentComp, visited, node):
- Insert node into currentComp
- Set visited[node] to true
- iterate child through adjList[node] and if visited[child] is false
- Call getStronglyConnectComps(adjList, currentComp, visited, child)
- In the kosarajuAlgorithm(adjList) function:
- Create a visited array equal to the length of adjList with all values as False
- Create an empty array toposortOrder
- Iterate node through all indices of adjList, if visited[node] is False
- Call topoSort(adjList, toposortOrder, visited, node)
- Set transposeGraph as getTransposeOfGraph(adjList)
- Set all the values in visited as False
- Create an empty array of components
- While toposortOrder is not empty:
- Remove the first element from toposortOrder and set it as a node
- If visited[node] is False:
- Create an empty list component
- Call getStronglyConnectedComp(transposeGraph, component, visited, node)
- Insert component into components
- Return components
- In the given function
- Create an array of empty arrays of size equal to n, called adjList
- Create an empty array inDegree equal to size n and set all its values to 0
- Iterate edge through edges and set u and v as edge[0] and edge[1]
- Insert v into adjList[u]
- Increase inDegree[v] by 1
- Iterate node from 0 to n - 1
- If inDegree[node] is not equal to length of adjList[node], return False
- Set stronglyConnectedComps as kosarajuAlgorithm(adjList)
- If the length of stronglyConnectedComps is greater than 1 return False
- Otherwise, return True
Time Complexity
O( N + M ), where N and M are the numbers of nodes and edges in the graph.
The complexity of making the adjacency list O(N + M) and calculating the in-degrees of all nodes is O(N + M). The Kosaraju Algorithm takes O(N + M) time.
Hence the total time complexity is O(N + M).
Space Complexity
O( N + M ), where N and M are the numbers of nodes and edges in the graph.
We maintain an adjacency list that will have O(N + M) items at most. The recursion depth of both DFS functions(topological sort and get connected components) is O(N).
Hence the overall space complexity is O(N + M).
Code Solution
(100% EXP penalty)
Eulerian Circuit
C++ (g++ 5.4)
Console



